讲解低通到高通的变换及高通滤波器设计方法

1、低通到高通的变换

由（5.1-9）式和表5.1-1，归一化二阶巴特沃思低通滤波器的传递函数为

将上式中的S用1/S进行变换，即得二阶巴特沃思高通滤波器的传递函数，其表示式为

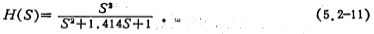
（5.2-10）式的传递函数可用图5.2-1a电路来实现，其元件值和电路结构如图5.3-8a所示。将图中的电阻R换成电容C，电容C换成电阻R，且变换后的电容、电阻值分别是原电路电阻、电容值的倒数。经过这样变换后的电路传递函数，就是（5.2-11）式，即由二阶低通变换为二阶高通，其电路及元件值如图5.2-8b所示。高通滤波器设计方法。图5.2-8c是图5.2-8a、b电路的幅频特性。由幅频特性可知，在低通止带衰减值As和高通止带衰减值As相间的条件下，低通止带角频率Ωs和高通止带角频率QsH的关系为：

式中fs为低通止带频率，fc为高通截止频率，fsH为高通止带频率。（5.2-12）式表明：可以先把实际要求的高通滤波器的衰减特性，变换成相应的归一化低通滤波器的衰减特性。

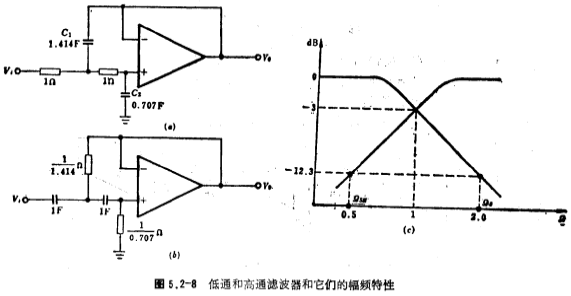
上述二阶巴特沃思滤波器的变换条件和变换关系式同样适用于高阶或其他类型的滤波器。

2、全极点高通滤波器

全极点高通滤波器通常由图5.2-1低通滤波器经变换后得到。因这种电路从低通转换到高通后，其电容值是相同的，并可以取标准值电容，给设计和制作者带来很大方便。下面通过设计实例来了解高通滤波器设计方法。

【例4】设计一个巴特沃思高通滤波器，主要参数：（1）截止频率fc=100赫兹；（2）止带频率fsH=33.3赫兹时，其衰减As≥60分贝。

解：      i.计算低通止带角频率Ωs：

由（5.2-12）式，Ωs为

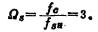
            ii.计算低通滤波器阶数n：

由（5.1-3）式，求得巴特沃思低通滤波器的阶数n：

              iii.确定低通滤波器的电路结构：

选用图5.2-1a二阶低通滤波器作为六阶低通滤波器的基本单元，其电路形式如图6.2-9所示。

           iv.由表5.2-1得各级的电容值：

第一级C1=1.035法拉，C2=0.966法拉。

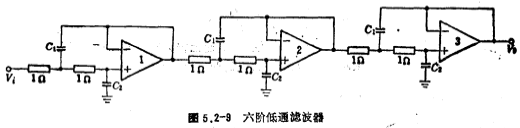
第二级C1=1.414法拉，C2=0.707法拉。

第三级C1=3.863法拉，C2=0.259法拉。

                v.将低通转换成高通；

由图5.2-9得六阶高通滤波器，其结构如图5.2-10所示。

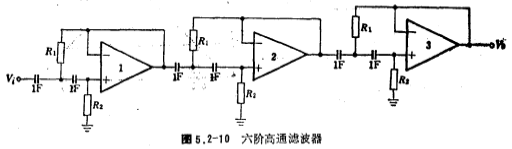
                vi.计算图5.2-10高通滤波器中的电阻值：

                根据转换关系式得

vii.对图5.2-10中元件值进行频率变换和尺度变换；

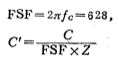
取C'=0.015微法，则阻抗变换因子Z为

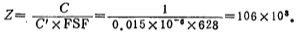
经R'=RZ变换后，其各级电阻值为

第一级R'1=0.966×106×10³=102千欧，

          R'2=1.035×106×10²=109.7千欧；

第二级R'1=74.9千欧，R'2=149.9千欧：

第三级R'1=27.5千欧，R'2=409.6千欧。

至此，计算和设计结束。

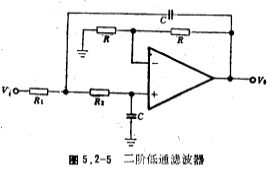
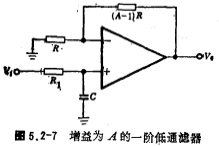
全极点高通滤波器也可由图5.2-7一阶低通滤波器和图5.2-5二阶低通浊波器经变换后得到，其变换方法与图5.2-1电路的变换方法相同。（5.2-1电路图文字此处点击）

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助