MOS运放有源低通滤波器设计及尺寸原理电路详解

1、二阶、三阶低通有源滤波器

图5.2-1a、b分别为二阶、三阶低通有源滤波器，它们构成全反馈形式，故有低的输出阻抗和高的输入阻抗，因此，这种电路在串级使用时，级与级之间没有影响，也就是说，以图5.2-1a、b电路作为基本单元，进行串级相连，可以方便地实现高阶低通有源滤波器。

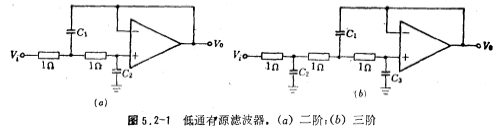
为方便起见，图中的电阻值均假定为1欧姆。

图5.2-1a二阶低通有源滤波器的传递函数H（S）为

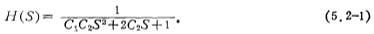
若选用归一化的巴特沃思低通滤波器，将（5.2-1）与巴特沃思网络函数（5.1-9）式进行比较，令两式的系数相等，这样可得

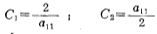
由表5.1-1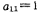，.414，代入上式，得

这里C1、C2的单位为法拉。

若选用归一化的为0.5分贝的切比雪夫低通滤波器，将（5.2-1）式与切比雪夫网络函数（5.1-23）式进行比较，令两式的系数相等，利用表5.1-5中的值，并经换算后，得C1和C2电容值为：C1=1.403，C2=0.470。

对于图5.2-1b三阶低通有源滤波器中的电容C1、C2和C3值，可用同样方法求得。

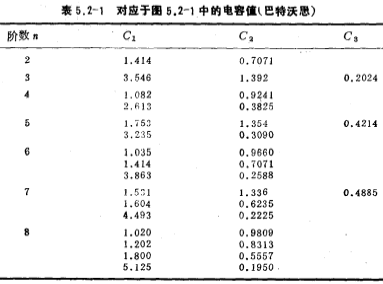
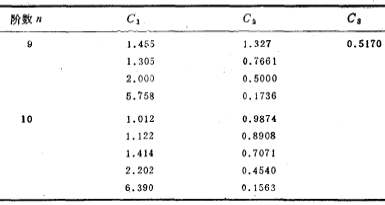
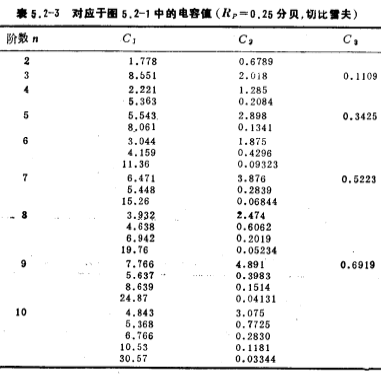
表5.2-1~4按巴特沃思和切比雪夫网络函数，列出图5.2-1低通滤波器中的电容值。

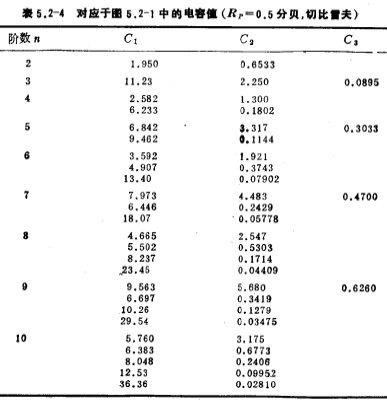
我们利用图5.2-1的电路和表5.2-1~4中的电容值，方便地设计出巴特沃思或切比雪夫低通滤波器。

【例1】设计一个归一化五价巴特沃思低通滤波器。

采用图5.2-1a、b所示的电路结构，将三阶低通滤波器与二阶低通滤波器相串联，构成五阶低通滤波器，其连接方法如图5.2-2所示。

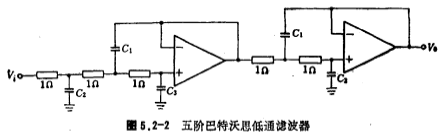
由表5.2-1，可以得到图5.2-2电路中第一级（三阶低通滤波器）的电容C1、C2和C3的值分别为：C1=1.753法拉，C2=1.354法拉，C3=0.4214法拉。同样，由表5.2-1可以得到该电路第二级（二阶低通滤波器）的电容C1和C2的值分别为：C1=3.235法拉，C2=0.3090法拉。

以上设计的低通滤波器，是在归一化频率条件下得到的，且选用的电阻值很小，而电容值又很大，不适合实际情况。因此，需要根据实际的工作频率进行频率变换，电路中的电阻、电容也要进行尺度变换。

2、尺度变换

设频率变换因子为FSF，其定义为

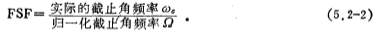
若低通滤波器的截止频率fc=100赫兹，归一化截止角频率Ω=1弧度/秒，则频率变换因子FSF为

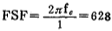
对于归一化的低通滤波器来说，其截止角须率Ω=1弧度/秒，若要转换到某一截止须率fc时，那么归一化低通滤波器中的电容值应除以频率变换因子值FSF。

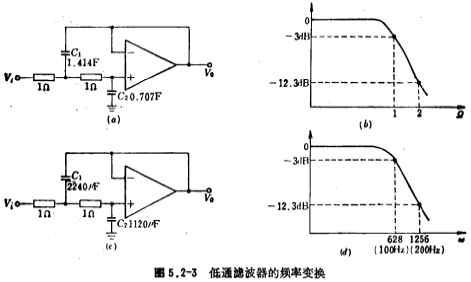
图5.2-3给出了频率变换的实例，图5.2-3a是二阶的归一化巴特沃思低通滤波器，图5.2-3b是它的幅频特性。图5.2-3（c）是截止频率fc为100赫兹的二阶巴特沃思低通滤波器，其电容值是图5.2-3a电路中的电容值的1/628，图5.2-3d是它的幅频特性。

除了进行频率变换以外，还需要对电阻值和电容值进行尺度变换。设阻抗的尺度变换因子为Z。如果我们把滤波器中的电阻增大Z倍，那么整个网络中所有的阻抗都应该增大Z倍，要使电容容抗增大Z倍，则应使电容值减小Z倍。因而，滤波器中的电阻和电容的尺度变换关系式为

现对图5.2-3c二阶巴特沃思低通滤波器中的电阻、电容进行阻抗尺度变换，若取Z=10000，则图中的电阻值R'=ZR=10千欧，电容值C1'=C1/Z=0.224微法，C2'=C2/Z=0.112微法。经阻抗尺度变换后，其幅频特性保持不变。

对频率变换和阻抗尺度变换进行综合考虑后，电阻和电容变换关系式为

【例2】设计一个增益为1的低通滤波器，主要指标为：（1）截止频率fc=100赫兹；（2）止带频率fc=350赫兹时，衰减分贝；（3）通带波动不大于0.5分贝。

解 i.计算止带归一化角频率Ωs：

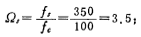
ii.选用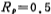分贝的切比雪夫低通滤波器；

iii.由（5.1-19）式求阶数n；

将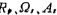值代入（5.1-19）式，得阶数n=5；

iv.选用图5.2-2的电路结构；

v.利用表5.2-4，得到归一化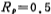分贝的切比雪夫低通滤波器。其第一级滤波器的电容值为

C1=6.842法拉，C2=3.317法拉，C3=0.303法拉。

第二级滤波器的电容值为

C1=9.462法拉，C2=0.114法拉。

vi.进行颜率变换和阻抗尺度变换；

FSF=628，取Z=5×10⁴。

第一级滤波器的电容值和电阻值；

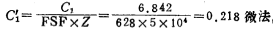
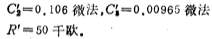
第二级滤波器的电容值和电阻值：

C1'=0.301微法，C2'=0.00363微法，R'=50千欧

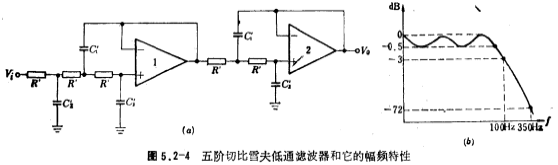
符合设计指标的低通滤波器及其幅须特性如图5.2-4a、b所示。

3、低通滤波器的设计

由上述讨论可知，利用图5.2-1电路可方便地设计出不同阶数的低通滤波器，但这种电路结构设计出的电容值往往偏离标准值，且电容值是各不相同的，这给设计、制作人员往往带来困难。为此，可选用图5.2-5的二阶低通滤波器电路，其增益为2。图中的电容值可由设计人员自己选定。要实现高阶（n为偶数）低通滤波器可将图5.2-5电路进行串联。

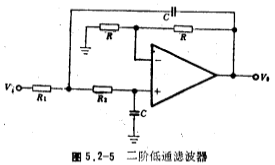
图5.2-5所示的二阶低通滤波器的设计公式为：

（1）确定电容值（由设计人员自己选定）

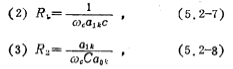
式中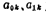为巴特沃思、切比雪夫网络函数的系数（见（5.1-9）、（5.1-12），（5.1-23）和（5.1-24）式），其值分别由表5.1-1~5图5.2-5二阶低通滤波器给出，对于巴特沃思低通滤波器，其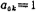；ωc为低通滤波器的截止角频率。

从（5.2-7）、（5.2-8）式得到的阻值不是归一化值，而是经过频率变换和阻抗尺度变换后的值。

【例3】设计一个通带波动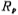为0.1分贝，截止频率fc为100赫兹的四阶切比雪夫低通滤波器。

解    i、选用图5.2-5的电路结构。其四阶切比雪夫低通滤波器的电路形式如图5.2-6所示。

       ii、选取电容C=0.01微法。

      iii、由表5.1-3得

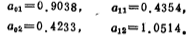
      iv、计算R1和R2；

第一级；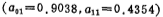

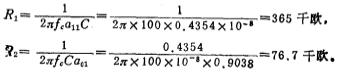
第二级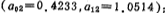

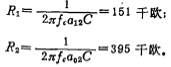
v、图中的电阻R可选取100千欧。

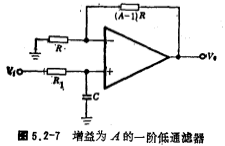
对于阶数为奇数的低通滤被器来说，一定有一个实极点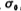，它可以由增益为A的一阶低通滤波器来实现，其电路形式如图5.2-7所示。图中的电阻值R1可由下式求得；

式中fc为低通滤波器截止额率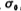，为实极点。上式得到的电阻R1值也不是归一化阻值，而是经过频率变换和阻抗尺度变换后的阻值。

对于巴特沃思低通滤波器，其实极点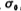=1，而切比雪夫低通滤波器其实极点可由表5.1-3~5中找到。

奇数阶低通滤波器可由图5.2-7电路与图5.2-5电路，或与图5.2-1a电路相串联来实现，即奇数阶低通滤波器的第一级是一阶低通滤波器，后面各级均是二阶低通滤波器。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助