解析MOS管高频小信号电容计算的强反型工作特性

强反型

在8.3节中，我们曾用对应于近似模型的电荷表达式来计算五个电容：Cgs、Cbs、Cgd、Cbd和Cgb，并曾给出了这些电容与VDS和BGS的几条关系曲线。MOS管高频小信号电容计算。我们可用同样方法来计算本节中已定义的新电容。MOS管高频小信号强反型。在推导这些电容的表达式时，我们还要利用8.3节中的简化假设，即δ=δ₁，δ₁由式(8.3.7)给出，以及dδ₁／dV_S和dδ₁/dV_B都可忽略。

在定义式(9.2.1b)中代入qD=QD[QD按式(7.4.19)计算]，可以求出Cgd。经过许多代数运算之后，求得

其中，α定义于式(4.4.31)，并绘于图4.13中。同样，可求得

以及利用式(7.4.15)，求得

把最后一个公式和式(8.3.12)进行比较可看出，对于采用我们作过简化假设的近似模型，有

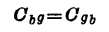
为了计算Csd，我们把式(7.4.20)的Qs代入定义式(9.2.1b)，从而得到

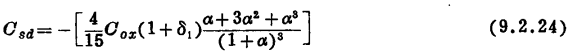
注意，在非饱和时，这个量为负，这与测量结果相符(饱和时，C_sd变为零)。对于这一负值，可以如下面那样直观地来考虑。漏端电压升高ΔVD，将使漏端的有效反向偏压增加，并将引起反型层电荷数量减少。MOS管高频小信号电容计算。由于QI是负的，因此这意味着变化量ΔQI>0，QI的这一正变化量将由正的ΔQs和正的ΔQD共同分担。所以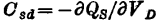，将是负的。

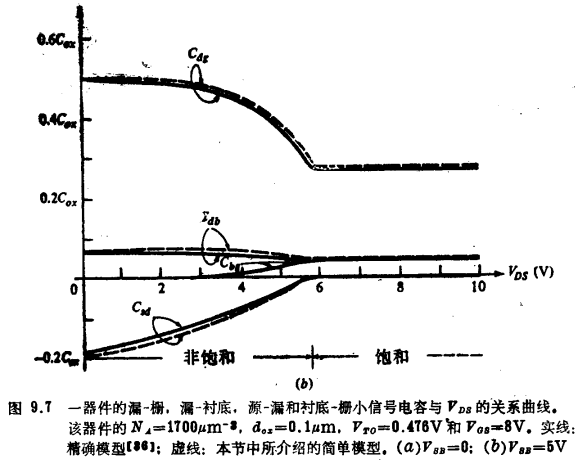
Csd、Cdg、Cdb和Cbg的曲线在图9.7中用虚线表示。实线表示采用通用电荷薄层模型的精确模型。正如对图8.14所做的那样，我们已把近似模型的饱和电压V´DS选得与精确结果一致。MOS管高频小信号强反型。这是可行的，因为近似直流电流式(4.4.30)中的δ假定选得与电容表达式中的δ1无关。可见，  当VSB较小时，除Cdb和Cbg之外，可以获得较高的精度(图9.7a)。如果像在8.3节中对Cbs和Cdb所做的那样，即用式(8.3.14)形式的一个函数来取代δ1，则Cdb和Cbg的精度可以得到改善。

上述关系式与式(8.3.8)至式(8.3.12)一起给出了九个电容：C_gs、C_bs、C_gd、C_dg、C_bd、C_db、C_gb、C_bg和C_sd。本节中所定义的其他任何电容参数都可从这些电容以及式(9.2.8)或式(9.2.20)求得。例如，利用后者我们求得

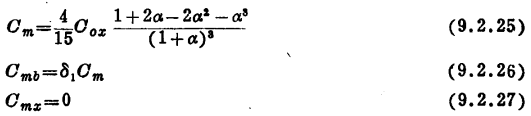
这样，我们就有图9.5模型中的所有九个电容参数的表达式了。在图9.8中用虚线给出C_m，C_mb和C_mx与VDS的关系曲线。实线再次表示精确计算的结果。VSB较小时，C_mb的精度欠佳。MOS管高频小信号电容计算。用式(8.3.14)形式的一个函数式取代δ₁可以改善它的精度。MOS管高频小信号强反型。然而，对于大多数应用来说，C_mb和C_db都不是最重要的参数。还要注意，简单模型预测C_bg=C_gb或C_mx=0。可是精确计算却得出

因而

但是，如图9.8中所示，C_mx非常小，在大多数实际情况下，它并不重要。

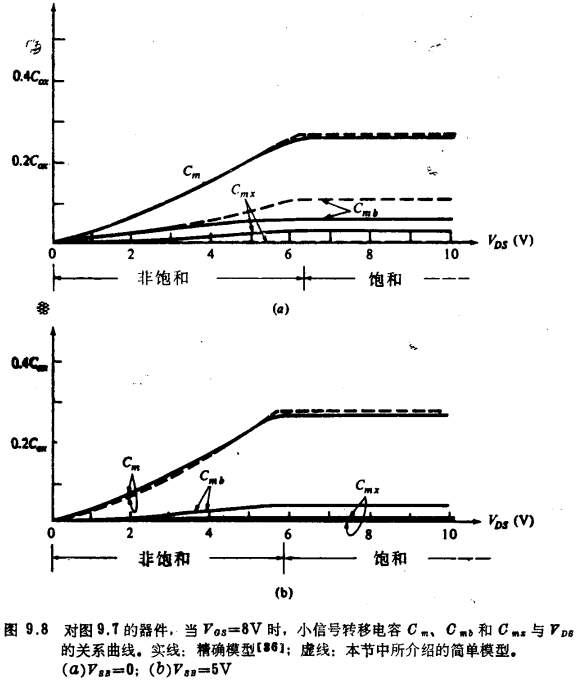
利用上面得出的结果和式(8.3.15)，可得[如果VDS较小和(或)VSB较大]

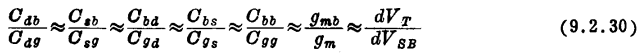
现在，我们来考虑在两种感兴趣的特殊情况下，电容参数的值。

VDS=0时的非饱和。在上述结果中，令VDS=0(a=1)，不难得到下列一些电容值(为完整起见，下面我们也重新写出8.3节中所得到的结果)。

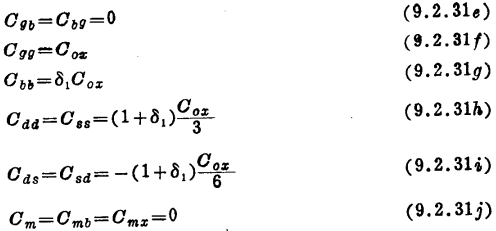
我们注意到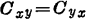，这里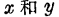表示s、d、g和b中的任意两个。实际上，这是真正能观察到所有电容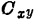都满足这一等式的唯一情况。MOS管高频小信号强反型。如果VDS≠0，则可发现，  一般情况下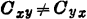，，其原因已经讨论过了。

上面有一些结果已在8.3节中获得并讨论过了。这里，我们将设法说明其余结果看起来也似乎有理。由3.4.2节可知，在沟道的源端和漏端，单位面积反型层电荷Q´I的值为

 其中

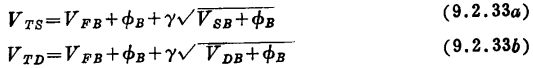
当然，这里我们对VDS=0的情况感兴趣。  然而，我们已经把VD和VS考虑为两个互相独立的电压，因此，在把有关的表达式对某一电压求微分的同时，可以保持另一个电压为常数，以便与电容的定义一致。

    当VD≈VS时，可以假设沿沟道方向，Q´I随位置劣成直线变化，即

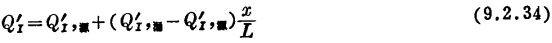
把上式代入式(7.3.9)可求得Qo和Qs,结果是

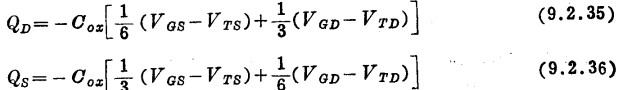
现在，利用上述表达式不难证明式(9.2.31)中各个电容的值是正确的。特别是在式(9.2.31h）和式（9.2.31i）的分母中出现3和6的原因，现在变得十分明显了。

式（9.2.31）中的所有结果和利用对应于精确反型模型的电荷表达式而得到的结果完全一致。

饱和

利用VDS=V´DS(α=0)的—般电容表达式，给出下列结果(有些结果已在8.3节中导出，为方便起见，重写于下)。

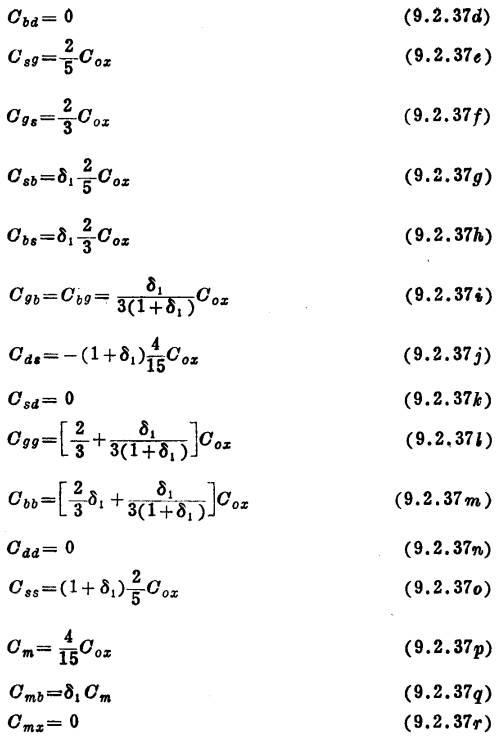
注意，在饷和时，正如已讨论过的那样，有

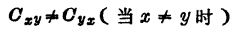
联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助