MOS管晶体管本征截止频率的中/强反型等效电路

考虑连接为如图8.16a所示的一个晶体管，假设其中的偏置电压使得管子工作在饱和区。电压源正∈sinωt是角频率为ω(rad／s)的一个正弦小信号。对于这种连接的小信号等效电路可以用图8.13的电路取代晶体管，并用短路线取代所有的直流电压源(由于这些电压源的ΔV=0)而导出来。现在，移去与短路线并联的所有元件，并注意饱和时，Cgd为零，就可得到图8.16b的电路。小信号漏端电流和栅电流可用这一电路来计算，并已直接表示在图上。如果定义电流增益αi为小信号漏端电流的幅值与小信号栅电流的幅值之比，则有

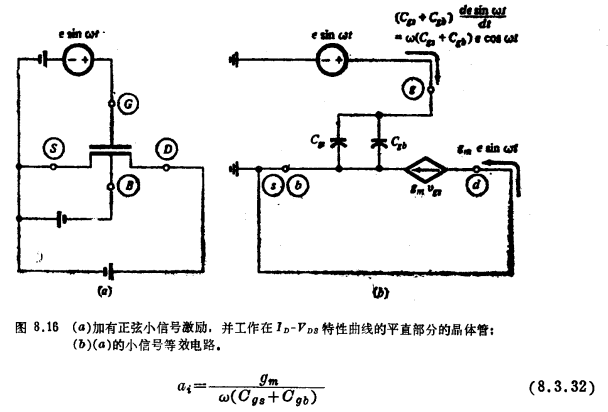
    当ω→0，上式变成无限大，这是意料中的，因为在直流时，没有栅电流。随着ω增加，αi下降。本征截止频率或本征最大可用频率，记住ωT，定义为αi(下降为1时的ω值。从式(8.3.32)可得，这个值为

利用式(8.2.8a)和式(8.3.27)，略去Cgb，我们得到：

其中ωo定义于式(8.3.6)。由于ωT的值在模型的有效区之外，所以，此值最初应看成一个可疑的结果。然而，用更高频率的模型(第9章)来计算ωT，给出了基本上相同的值。其原因是上述计算只涉及电流的大小。因为这一点，所以在这些频率上，使用简单模型所引起的误差是不大。不过，在这样高的频率上，使用本章所导出的模型可导致显著的相位误误差。

作为一个例子，考虑一个晶体管，它具有μ=60／μm²／(V·n3)，L=6μm以及δ=0.2，工作饱和区，并设VGS-VT=2V。从式(8.3.34)，有ωT=4167Mrad/s，  对应的fT=ωT／2π=663MHz。

实际上，因为存在非本征的寄生元件(8.4节)，一个完整的品管体在小于ωT的某一频率时，电流增益变为1。

中反型

在7.4.3节中已提到，在推导各种电荷表达式时，中反型区可以忽略。在这些情况下所采用的方法是，认为弱反型和强反型的电荷表达式在互相紧挨的两个区中有效。对于电荷计算来说，产生的误差常常是可以接受的。但是，在预测电容时，这样的电荷表达式会导致较大的误差。在本节的后面部分将可看到这一点，那时我们要把上面的方法与适用于所有反型区的复杂的通用模型所导出的结果进行比较。

对于其他参数也有同样的情况，在中反型区，没有简单的，显式的电容表达式可用。

弱反型

在弱反型时，情况十分简单。在整个沟道长度上反型层电荷可以忽略，从而栅通过氧化层可以直接“看到”耗尽层。VB的一个微小增量会引起一些空穴通过衬底端进入器件，而这将被通过栅端离去的某一栅电荷所平衡。相应的Cgb值可用从式(7.4.34)得到的弱反型时的QG代入式(8.3.5)求得：

弱反型时，改变Vs或VD可使反型层电荷在相对意义上急剧地变化。然而,与QG和QB相比该电荷仍可忽略，故在电荷平衡过程中不起任何作用。因此，栅和衬底都“感受”不到VS和VD的变化，因而在图8.11b和c中，ΔQG和ΔQB可以忽略。对应的电容值于是便为：

对于弱反型(VDS>5Φt)，本征截止频率可以用与在强反型时类似的方法来定义，  且图8.16仍然有效。把式(8.3.36)代入式(8.3.33)，得到

利用弱反型时的gm和Cgb的表达式，可以证明

式中，ID是在特定工作点上的电流，IM是弱反型时可以达到的最大电流(即在弱反型区的上限点的电流)。

作为一个例子，考虑一个μ=60um²／(V·ns)及L=6μm的器件，工作在室温下，ID等于最大反型电流的1／5°于是，式(8.3.38)给出ωT=8.7Mrad/s，这对应于fT＝ωT／2π=1.38MHz。在前面知道，同一器件在VGS-VT=2V，强反型时，fT是663MHz。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助