电子技术论坛
信息来源: 时间:2022-7-29
MOS管晶体管低频小信号的通用模型重要性
在4.3节中已说明,对于长沟道器件(忽略沟道长度调制效应)可导出适用于所有工作区的一般表达式[式(4.3.8),(4.3.16)和(4.3.17)]。这样一类表达式可用来提供小信号电导的表达式,该表达式将适用于包括中反型在内的所有工作区和强反型时从非饱和到饱和的过渡区。当然,这里的困难将是公式的复杂性。式(4.3.16)的漏端电流公式中显式地包含了VGB,通过ψSO和ψSL也隐含了VGB[见式(4.3.18)]。 当企图对VGS微分时,这就需要作一些代数运算。然而,已有人建议用下面的近似式,以得到较好的精度:

其中ψSO和ψSL是沟道源端和漏端的表面势,可按式(4.3.18)来计算。作为检验,在强反型这一特殊情况下,代入ψSL≈ΦB+VDB以及ψSO≈ΦB+VsB就可导出式(8.2.6a)。 在弱反型时,由于此时ψSL和ψSO近似相等,如果要使用式(8.2.40),则必须要当心。
有了一个对所有区域都有效的gm模型,就可以绘出当ID在大范围内变化时,gm的曲线图,在图2.9中,假设VSB不变,对于不同的W/L值及工作在ID-VDS特性的平直部分情况下,绘出了loggm与logID的关系曲线。对于每-1W/L值,右边的直线段对应于强反型,左边的直线段对应于弱反型,弯曲部分对应于中反型。在强反型区,对于一给定的ID值,若用较大的W/L值,则可获得较大的gm,正如从式(8.2.6b)所预期的一样。然而,在弱反型区就不是这样了,正如在图中以及从式(8.2.35)所见的一样。这里,ID一旦固定,gm也就知道了(记住,在目前的讨论中,VSB是固定的,因此n是固定的)。这一特性在图8.9中与双极器件的特性作了比较, 对一给定的ID值,MOS晶体管在弱反型时gm是双极晶体管对应值的1/n。
4.3节中的通用模型也可用来推导(不计沟道长度调制效应和短沟道效应)对所有区域都有效的gd值。可以指出①,有

因此,利用式,可得

作为验证,现在来考虑非饱和区。上式中,把VDB+ΦB=VDS+VSB+ΦB代入ψS可以得出式(8.2.17)。在从非饱和到饱和的过渡区内,使用精确的中ψSL值可为长沟道器件提供精确的gd值。
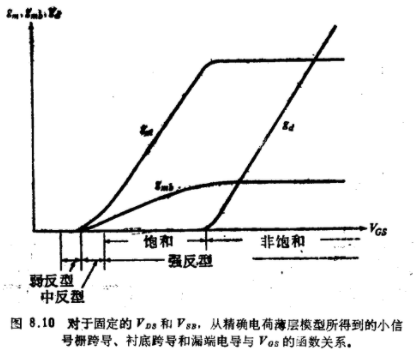
对于固定的,较大的VDS,gm、gmd和gd与VGS的关系曲线具有如图8.10所示的形状。这样一些曲线表明,这些量在所有反型区都是连续变化的.随VGS的增大,所遇到的各不同区域的顺序在第7章中已结合图7.8讨论过了。
联系方式:邹先生
联系电话:0755-83888366-8022
手机:18123972950
QQ:2880195519
联系地址:深圳市福田区车公庙天安数码城天吉大厦CD座5C1
请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号
请“关注”官方微信公众号:提供 MOS管 技术帮助