电子技术论坛
信息来源: 时间:2022-7-26
MOS晶体管准静态模型的局限性及其重要性分析
根据迄今为止的讨论可知,如果端电压变化足够慢,以致使沟道内电荷的分布可以忽略其惯性,能够跟上电压的变化,则我们可预期准静态模型将是有效的。给出“足够慢”的定量定义是难以做到的,从利用准静态模型得到的结论是否可信,取决于施加在端极上电压波形的类型,器件的工作区,所要求的结果的类型(例如电流波形的形状、延时、上升时间等)以及所追求的精度等等。实际上,利用示于图7.11a的一种简单而又基本的情况,已半经验地导出了一些比较粗糙的规则。如图7.11b所示,这里只有vG是变化的。如式(7.3.4a),漏端电流包含了传输分量iT(t)和充电分量iDC(t):

对于数字电路应用中的近似计算,常常假设: 若VGS<VT,晶体管处于截止状态;若VGS<VT,晶体管处于强反型状态。采用这一简化假设意味着器件在t=t1时突然从截止变为饱和。我们也假定VDD足够大,以致器件从不进入非饱和状态。电流的传输分量可从任意一种直流模型求得,并示于图7.11c,其充电分量iDC(t)可从式(7.3.16a)求得。由于υD、υS和υB杯是常数,式(7.3.16a)给出

在饱和区,准静态工作下的qD值QD, 由式(7.4.28)给出,这样
由式(7.4.28)给出,这样 为-
为- ,这是一个与υG无关的负常数(尽管在更一般的情况下,可期待偏导数∂qi/∂υi是端电压的函数)。 由于dυG/dt对于υG的上升部分是恒定的,故iDC(t),具有如图7.11d所示的波形。
,这是一个与υG无关的负常数(尽管在更一般的情况下,可期待偏导数∂qi/∂υi是端电压的函数)。 由于dυG/dt对于υG的上升部分是恒定的,故iDC(t),具有如图7.11d所示的波形。
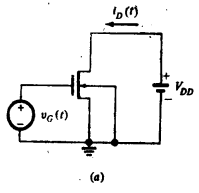
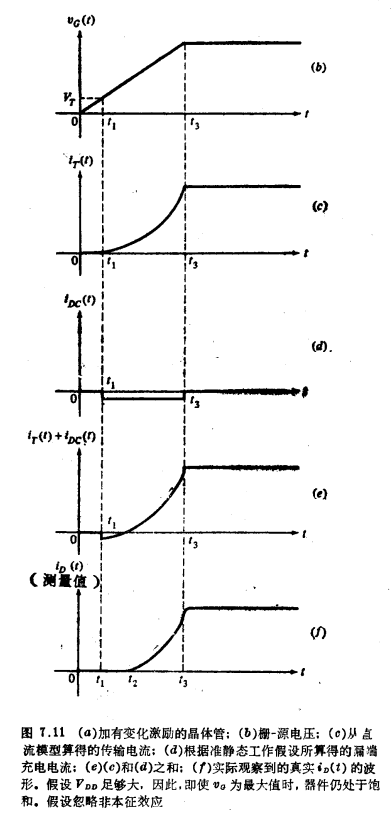
把两个漏端电流分量相加,便得出iD(t),如图7.11e所示。
假设忽略非本征效应,通过测量发现iD(t)的波形如图7.11f所示[19-21]。可见,这波形不同于图7.11e所示的“准静态”结果,特别在以下两方面:
1、在t=t3时,图7.11e中的波形预测iD(t)立即跳到其直流稳态值,这是假设电荷无惯性,能自动调节的结果。实际情况并非如此,而是如图7.11f所示。t=t3时,在图7.11f中可以看到有一点“弯曲”。其原因如下:在t=t3之前,增加VG要求沟道中有越来越多的∣q´I∣,所以源提供的电荷只有部分能流出漏。一旦υG停止增加,由于沟道填充电荷的过程已经完成,因而源供给的所有新的电荷都可流出漏。这样,t=t3时,iD( t)曲线的斜率有显著的变化。
2、在t1之后的一段时间,准静态模型预测漏端电流是负的。实际上,一旦抽去非本征器件效应,这一现象就观察不到了。实际情况却是如图7.11f所示,在时间t2以前,漏端电流一直为零。这一点可解释如下:t<t1时,沟道是空的。在t=t1时,沟道中的状态变为对电子有利,于是电子由源进入沟道,并向漏移动。可是,在电子到达漏以前将观察不到漏端电流。电子到达漏的时刻为t2,如图7.11f所示。与此相反,准静态模型假设在t1之后的任意时刻t´,整个沟道长度上布满电子,和υG长时间地固定为υG(t´)值时的情况一样,即认为电子到达漏是不需要时间的。这里,与图4.15d的流体动态模拟(相当于饱和区)进行比较将是有益的。假设最初活塞的位置足够高,使得两池之间的联系被切断,没有流体进入通道。现在活塞快速向下移动( 增加),t=t1时,
增加),t=t1时, 移过固定值移
移过固定值移 (回想一下,这相应于晶体管VT≈0的情形)。活塞最终停在如图所示的位置。在t=t1时,流体开始从源池进入通道,但是流体将在t1以后的某一时刻到达通道的右端并泻入漏池。而准静态模型相当于在任意时刻t´(>t1),流体就布满整个通道, 且其分布情况对应于活塞的某一固定位置
(回想一下,这相应于晶体管VT≈0的情形)。活塞最终停在如图所示的位置。在t=t1时,流体开始从源池进入通道,但是流体将在t1以后的某一时刻到达通道的右端并泻入漏池。而准静态模型相当于在任意时刻t´(>t1),流体就布满整个通道, 且其分布情况对应于活塞的某一固定位置 (t´)①。这一现象还将在7.7节中再来考虑。
(t´)①。这一现象还将在7.7节中再来考虑。
当要求预测漏端电流波形的细节时,准静态模型就失效了。然而,在许多应用场合,这不会有很大影响,因为波形的细节常常没有多大价值。例如,在大量数字电路设计中,感兴趣的量是初值、终值、输出的上升或下降时间、输出与输入之间的延时等等。与测量结果以及与非准静态数值结果进行比较后指出,在大量的数字电路的分析工作中,准静态模型可以采用,所得结果是可以接受的,只要波形的上升时间tR②满足条件[20,21]

其中τo由式(7.5.4)给出,该式中的VGs采用图7.11b中υG(原文中为VGS,显然有误。——译者)的最大值。这里要着重指出,上述做法仅仅是一种粗糙的方法③。例如,式(7.6.3)中的系数20也可改用15或25,可视应用情况而定。作为一个说明他tR数量级的数字例子,我们来考虑一个μ=64μm2/(V·us),VT=1V,L=4μm,δ≈0以及VGS,max=5V的器件。对于这一器件,式(7.6.3)所要求的tR>1.25ns。
在普通的“基片”制造工艺中(第10章,用这种工艺制造的晶体管具有显著的非本征寄生电容),上述下限值不受限制,由于这些“分布”电容,芯片上内部波形的上升时间常常大于这一下限值,所以采用这些工艺时,晶体管的工作速度减慢了。除此之外,甚至在栅电压波形的上升时间偶尔略小于这一下限值时,但由于被驱动器件的分布电容,总的瞬态电流和延迟时间还会很大,因而会掩盖由于用准静态模型预测本征效应而产生的误差。采用诸如(cossilicon on sapphire)或介质隔离这样一些能减小分布电容的工艺,上述问题就不会发生。在这些情况下,以及在利用基片技术设法提高速度极限的情况下,应该带着怀疑的眼光来看待用准静态模型所得到的结果。
当晶体管工作在准静态模型失效的速度时,模拟这种晶体管的一种方法是把晶体管分成几段,每一段足够短,因而可用准静态模型。这一思想示于图7.12。在(b)中,每一方框假设为一个“子晶体管”,具有自己的想象的源点和漏点。当然,除最左和最右的那两个以外,其余的这些子晶体管假设都仅由本征部分组成,换句话说,假设中间的子晶体管不存在非本征的源区和漏区。
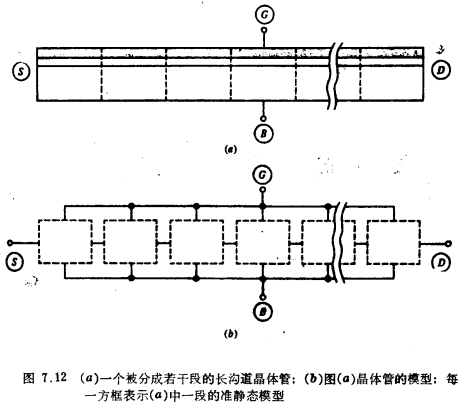
注意,在上述讨论中,我们没有考虑短沟道效应。短沟道效应会使这种描述大大复杂化。对晶体管(但还不是真正的长沟道器件)所观察的现象中,有瞬态传输电流(除瞬态充电电流之外),当然还有反映在式(7.4.1)中的速度饱和现象,以及建立在式(7.4.1)成立基础上的一些关系式。在这一情况下,二维数值模拟是一种有用的工具[19.20]。最后,还有另外一种与短沟道效应无关的现象,在我们的建模中还没有考虑。这一现象了再栅电压波形下降时观察到。由于υG(t)减小,因而电子要通过源端了漏端出去,在这一移走过程中,电子就会穿进体内。在那里它们与空穴复合,造成衬底电流流动。这种现象称为“电荷抽出(charge pumping)”。凭直觉可以想象,对于具有较短下降时间的栅电压波形,!这一现象会更显著。据估计,对于3μm长的器件,当下降时间是0.4ns或对10μm长的器件,当下降时间约为1ns时, 1%的总反型层电荷会通过衬底流出。
在结束本节时,我们提醒读者,与器件非本征部分有关的寄生元件会大大地改变晶体管的特性(与本节预测的特性相比)。寄生元件包括栅-源和栅-漏的重迭电容;以及衬底-源和衬底-漏的结电容。加之,衬底不是理想的良导体,它的显著的电阻和本征电容及非本征衬底电容结合在一起会影响器件的动态特性。
联系方式:邹先生
联系电话:0755-83888366-8022
手机:18123972950
QQ:2880195519
联系地址:深圳市福田区车公庙天安数码城天吉大厦CD座5C1
请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号
请“关注”官方微信公众号:提供 MOS管 技术帮助