电子技术论坛
信息来源: 时间:2022-7-18
MOS晶体管强反型准静态工作下电荷的计算分析
在准静态工作假没下(7.2节),可直接推导出计算式(7.3.16)中的充电电流所需的电荷表达式。在此假设下,我们可观察到,用υG(t)、υB(t),υS(t)和υD(t)来表示的qG(t)、qB(t)、qI(t),qD和qS(t)的表达式与直流条件下用直流电压VG,VB、VS和VD所表示的电荷QG、QB、QI、QD和QS的表达式是相同的,后者已在式(7.2.3)和(7.3.9)中以积分的形式给出了。如果对每一工作区单独进行讨论,则除中反型区外,从这些积分都可导出电荷是端电压的简单函数。这一内容将在下面几小节中阐述。利用4.3节中的通用电荷薄层模型,也可进行更一般的电荷计算,这一内容概括在7.4.5节中
非饱和的一般表达式
由于没有单位面积电荷与x的函数关系式,式(7.2.3)和(7.3.9)中的积分。因此,我们首先把变量x变换为VCB,VCB是反型层中x点相对于衬底的强反型“有效反向偏压”。从式(4.4.12)有:

利用此式,变换式(7.2.36)中的积分变量,从而给出:

与此类似,式(7.2.3c)变为:

以及式(7.2.3a)变为

根据式(7.3.9),QD和QS变为

最后,为把上述方程中的x用VCB来表示,我们对式(7.4.1)从x=0到沟道中任意一点x进行积分,有:

其中UCB是虚设的积分变量。一个与上式等价的结果已在4.4.3节中获得。这样,从式(4.4.37)有

其中h表示在非饱和区的漏端电流表达式:

中与W/L相乘的那个函数。
不难证明,式(7.4.5)与(7.4.4)是等价的。
饱和的一般表达式
把晶体管进入饱和时的VDB值记作V´DB;由于假定沟道较长,因而如果VDB在V´DB以上再增加,则沟道中的情况实际上不受影响。这样,例如,令gI(VGB,VSB,VDB)表示QI在非饱和时的表达式[它是对式(7.4.2c)求积分所得的结果],则有:

对QG、QB、QD和QS可写出相应的关系式。
利用上述结果,可以求得不同复杂程度的QG、QB、QD和QS的表达式。这些表达式的复杂程度取决于Q´G、Q´B、Q´D和Q´S和ID模型的复杂程度。
近似模型
根据4.4.2节中导出的在计算上是高效率的近似模型,可得出下面的漏端电流表达式:

其中

式中的α是一个参数,该参数按照使式(7.4.8)在非饱和及饱和时都成立的原则来定义:

式中

参数α已绘制在图4.13中。
为推导上述模型,4.4.2节中曾用下列表达式来表示非饱和时反型层和耗尽层的单位面积电荷:

这样,把上面两式代入式(7.4.2c)和(7.4.2b)便能求出相应的非饱和时的总电荷。利用式(7.4.10)所定义的简便参数α,我们可把这些结果表示为一种对非饱和与饱和均有效的形式。经过一些代数运算后,可得:


从式(7.4.2a)可求得总的栅电荷。然而,由于QI和QB都已求出,因而把上述两式代入下面的电荷中性方程来求QG更为简单:

其中Qo是总的等效界面电荷。所得结果为

为了根据式(7.4.3)求出QD和QS,需要知道x与VCB的关系, 这可由式(7.4.4)或(7.4.5)得到

把此式和式(7.4.12)代入式(7.4.3),并把结果推广到包括饱和区,我们得到

与此类似,利用式(7.4.3)可求得Qs。然而,利用式(7.4.14)和(7.4.19),从Qs+QD=QI来求Qs更为简单,所得结果是:

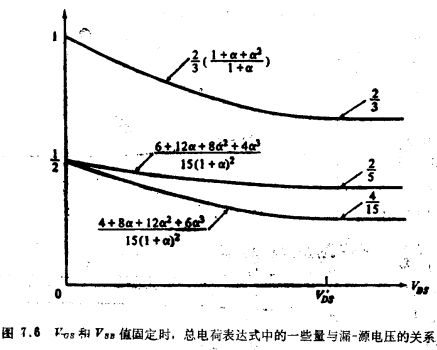
把出现在式(7.4.14)、(7.4.15)、(7.4.19)和(7.4.20)中的某些量绘成曲线示于图7.6,可见,尽管表达式看起来相当复杂,而曲线形状却非常简单。读者可能想要推导更简单的口的函数式,且这些函数式能准确地逼近这些曲线。
作为对上述计算方法的检验,让我们来确定VDs=0(α=1)时的电荷:
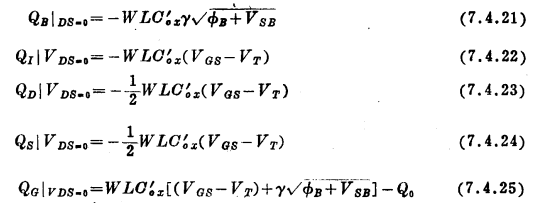
这些方程是有意义的。由于VDS=0,耗尽区内单位面积电荷是均匀的,且由式(7.4.13)(令VGB=VSB)给出。把这一结果与沟道面积W/L相乘使得式(7.4.21)。与此类似,令VCB=VSB,式(7.4.12)所给出的单位面积均匀反型层电荷,乘以沟道面积便是式(7.4.22)。QD和QS可见都是QI的一半,这是讲得通的,因为具有对称性。最后,式(7.4.25)可以从该式前面的几个方程和式(7.4.16)导出。
在饱和区(α=0),我们得到
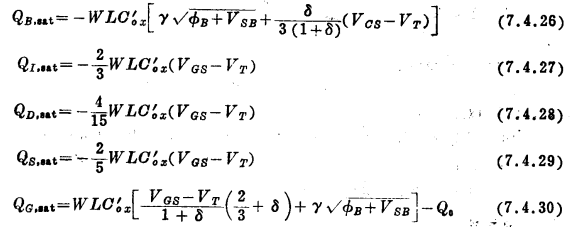
可见,上面这些电荷没有一个与VDS彦有关。这表明,在饱和情况下,由于夹断现象,漏对器件本征部分不再有任何影响(当然短沟道效应除外)。一端的电压对另一端电荷的影响一般说来是不可互换的。例如,在饱和区,假定VS、VB和VG固定不变,而VD变化。由于式(7.4.30)与VD无关,因而栅电荷将保持不变,故观察不到瞬态栅电流,还是在饱和区,但现在改为假设VS、VB和VD不变,而VG变化。根据式(7.4.28),显然QD将要变化。因此,除传导电流外,还有非零的“充电电流”流过漏端。从式(7.3.16a)和(7.3.16b)可明显看出这些事实。一端电压对另一端电荷的非交互影响,虽然在饱和时最为显著,但在非饱和时也是明显的,只有当VDS=0时,这一现象才消失。
这里我们注意到,在饱和区,有时假设QD等于零。这可用在饱和区沟道和漏是隔离的来说明。可是,正如已经证明过的,这种隔离仅仅是使iG保持与υD无关。事实是,当υG(t)变化时,iD(t)也会变化,并且没有理由假设这一变化中不包括充电分量iDC(t)(73节)。事实上,测量和数值模拟均表明,饱和时iDC(t)确实不为零。于是根据式(7.13.6c)可知,qD必须是这样的,即能够给出正确的IDC(t)。如果qD恒等于零,则就不可能给出正确的iDC(t)。所以,饱和时QD不为零。如果QD按7.3节中的说明来解释,则因夹断而造成的“隔离”和QD不为零这两者之间就没有矛盾了。
以VGS为参数,总电荷与VDS的函数关系曲线示于图7.7。
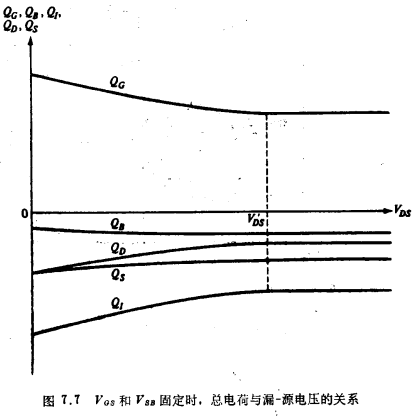
我们迄今所给出的电荷表达式,对于大多数准静态的瞬态响应计算是适用的。
精确模型
通用力程(7.4.2)和(7.4.3)可用来推导与4.4.1节中的精确模型相对应的电荷表达式。在这种情况下,我们必须借助于在推导精确模型时所用的单位面积电荷[由式(4.4.15)和(4.4.16)给出],导出的电荷表达式具有引人注目的特点,即它们对于VSB和VDB是完全对称的,这和4.4.1节中对应于精确模型的电流表达式一样。可是,这些表达式相当复杂,尤其是QD和Qs的表达式极其复杂,因而必须求助于近似方法。
联系方式:邹先生
联系电话:0755-83888366-8022
手机:18123972950
QQ:2880195519
联系地址:深圳市福田区车公庙天安数码城天吉大厦CD座5C1
请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号
请“关注”官方微信公众号:提供 MOS管 技术帮助