电子技术论坛

与衬底反型的注入沟道MOS晶体管的电荷及临界电压

信息来源：时间：2022-7-14

与衬底反型的注入沟道MOS晶体管的电荷及临界电压

电荷及临界电压

现在考虑p型衬底，n型注入的器件。在所有的注入离子（施主）最终都留在表面这样一种假设下，这些离子只是是使单位面积有效界面电荷Q´o改变了（+q）M，其中M是有效剂量；因此VTO下移qM/Q´o。然而更实际一些地说，注入的分布看来还是如图6.2a所示。这一分布上还是用6.2b来近似[这里N（）和NI表示施主浓度]。当NI>NAB时，表面和之间的区域可以看成是均匀掺杂的n型区域，其有效施主浓度为

MOS晶体管的电荷及临界电压

现在，我们来分析具有上述类型注入的器件。这类器件的工作情况相当复杂，所以要求读者有耐心。

电荷及临界电压

首先再来考虑图6.1b的三端结构。在某一固定的VCB值和各个不同的VGB值的条件下，这个结构的栅下半导体中的状态示于图6.8；图中的细节问题不久就要说明。因为VCB是固定值，所以n注入区-p衬底结的耗尽区画成是固定宽度的。注意，为了面单起见，n⁺区边界周围的耗尽区没有画出。由于NDS不必比NAB大很多，因此可以利用附录C中得出的双边阶跃结来求该结海边的单位面积电荷的大小，我们不难得

MOS晶体管的电荷及临界电压

式中单Φo为该结的自建电势，F=（2q∈s）。

我们将按由大到小的顺序讨论图6.8中VGB的影响。现在暂且忽略图中的Qn1，Qn2和Qn3。在图6.8d中，VGB假定大到足以把电子吸引到了表面；对nL型区域来说，这是一种积累状态。如果把VGB减小到这样一个值，即所有电子都离开表面，使表面成为中性，这就是图6.8c所示的状态。假如VGB在上述值之下再减小，这将使Q´G-Q´O成为负的(Q´G是单位面积栅电荷，Q´O是单位面积有效界面电荷)，为了平衡这一电荷，施主原子在表面必须耗尽，如图6.86所示。最后，随着VGB进一步减小，顶部耗尽区不断加宽，直到与pn结的耗尽区相遇为止，如图6.8a所示， ·

令Q´T为表面之下的那一层内的单位面积电荷(既可由施主原子也可由电子产生)。电荷平衡要求

注意,底部耗尽区内的电荷为Q´B -Q´B=0，因而上式中不出现Q´B。沿着从栅端，通过器件到衬底端这样一条路径可以写出电势平衡方程：

MOS晶体管的电荷及临界电压

式中，ΨT为顶部耗尽区两端的电势差，如图6.86所示，ΦO+VCB为注入-衬底结的耗尽区两端的总电势降落，如图6.86所示[参看式(1.5.12)]，ΦMS总是为栅和非注入P型衬底材料的功函数差引起的电势差。和式(3.2.4)一样，我们还有

MOS晶体管的电荷及临界电压

为了求解四个未知量(Q´G，Q´T，Ψox和ΨT)，还需有第四个方程。如果分以下两种情况来考虑，则不难建立这个方程。

MOS晶体管的电荷及临界电压

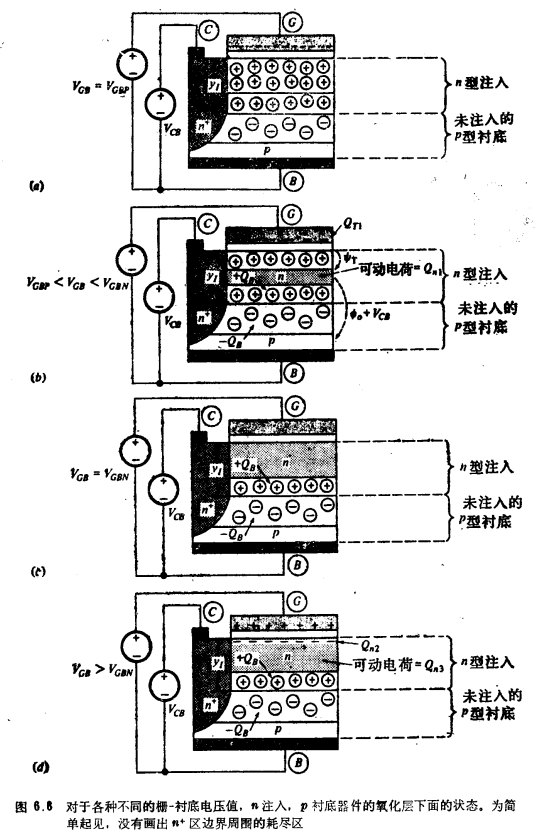
1、表面耗尽，图6.86。这里，QT由电离施主原子产生，所以是正的。这一状态与在p型衬底中已经遇到过的耗尽状态相反，因而图6.8b中所标的电势吵r带有负号。现在，我们可以利用类似于式(3.2.5a)这样的关系式，但是有些正负号必须适当地加以改变：

MOS晶体管的电荷及临界电压

式中，F=（2q∈s）^1/2。利用式(6.3.3)至(6.3.6)，可得：

MOS晶体管的电荷及临界电压

现在来讨论图6.8b中两个耗尽区之间的这一区域。由于电离杂质原子被符号相反的运动载流子所“补偿”(1.2节)，所以这个区域是中性的。它对电荷平衡方程式(6.3.3)没有贡献。这个区域又是n型的，其中的有效施主浓度NDS雳由式(6.3.1)给出。如果这个三端结构成为晶体管的一部分，则上述区中的运动电子可对电流的导通作出贡献。为了今后的用途，现在来计算这些运动电子的单位面积的电荷Q´n1。如果不存在耗尽区，则运动电子数将等于有效的施主原子数。因此，Q´n1将等于-q，其中=NDSI。可是，现在有些施主原子已经耗尽。因为耗尽一个施主原子就减少一个电子，所以电子总数减少了。剩下的运动电子电荷为

MOS晶体管的电荷及临界电压

现在，通过令Q´n1=0，并利用式(6.3.2)和(6.3.7)可以确定两个耗尽区相遇(图6.8a)时，VGB的值VGBP。所得到的表达式具有下面的形式：

MOS晶体管的电荷及临界电压

式中

MOS晶体管的电荷及临界电压

其中，VFB=ΦMS-Q´O/C´ox，以及

MOS晶体管的电荷及临界电压

上式中的γ是同一p型衬底上的非注入器件的体效应系数。因此，从式(6.3.10)可以看出，夹断电压Vp随VCB的增加而增大的情形与非注入器件的阈值电压相似，只是这里的有效体效应系数γI，大于γ。

如果VGB增加到足够大，则表面耗尽区将会消失，如图6.8c所示。这时表面是中性的，Q´T=0，因此ΨT＝0。利用这些观察结果和式(6.3.3．)至(6.3.5)，可以得到相应的VGB值，记作VGBN：

式中

MOS晶体管的电荷及临界电压

不难看出，VFBN实际上就是由栅，绝缘层和n型注入区(假定是均匀的)组成的这一结构的平带电压。

从迄今为止的分析可知，当VGB满足时，两个耗尽区之间存在一个非耗尽区，如图6.8b所示。当这个非耗尽区是晶体管的一部分时，它能导通电流。因为它位于表面之下，而不是紧挨表面，所以称它为埋沟。为了今后使用方便，我们把形成埋沟的条件表示为图6.8b中栅端和C端之间的电压。把式(6.3.15)中的VGB写成VGB=VGC+VCB，并利用式(6.3.9)和(6.3.13c)，可得

MOS晶体管的电荷及临界电压

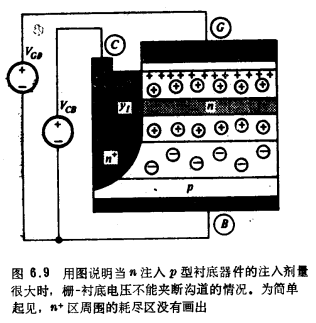
在结束表面耗尽的讨论之前，附带说明一种不希望出现的特殊情况。对于给定的NI和VCB，I较大的器件将需要更负的ΨT，以达到图6.8a中所说明的夹断状态。如I太大，则ΨT必须达到这样一个·值，即在实现夹断之前，就出现表面反型, 如图6.9所示。 (注意，注入是n型的，所以反型层由空穴组成。)一旦这一反型变为强反型，则表面势和顶部耗尽区的宽度就不会随VGB有明显地改变。和非注入器件中的情况一样，它们将被钉扎在某一值上。这样，通过将VGB变得更负来夹断器件就成为不可能了。这时，夹断只能依靠增加VCB来实现，也就是说，增加VCB，使底部的n注入区内的耗尽区不断加宽，直到它与顶部耗尽区被钉扎的边缘接触为止。为了避免发生上述问题，要求器件即使在VCB=0时也能夹断，并避免同时采用大剂量和高能量的注入。