分析与衬底同型的注入分段二次强反型模型

我们可以对电流公式进行简化，从而导出—个与式(4.4.30)有关的近似模型。利用类似于导出式(4.4.30)的方法，或者干脆直接通过式(6.2.27)的一种适当的展开式，便可得到这种简化模型。但是，这里必须使用两个不同的δ参数：与注入区有关的δ1和与非注入衬底有关的δ2。详细过程概括在题6.2的说明中。我们发现，在这样一种模型中，重又得到了下面形式的非饱和的电流：

只是其中的Ii(VK，VN)为：

式中VT，=1，2由式(6,.2.23)给出。参数δ1和δ2必须仔细地加以选择，因为它们本是VDB过临界值VI时，保证ID-VDB特性曲线斜率的连续性的关键参数。我们不希望斜率出现间断点，因为这将导致小信号参数的不连续性，从而使模型用于电路分析的计算机程序时产生数值问题。这—点将乍题6.2的说明中进一步讨论，该题中，建议δ1和δ2用下列值：

使用δ1的表达式时，应该谨慎从事，因为当VSB十分接近VI，表达式中将出现一个几乎相等的两数之差的比值，这个比值可能会损失数值精度。当VSB=VI，式(6.2.37a)成为不定式，此时可用它在该点的极限来代替。

    不难证明，

这可能是意料中的，因为δ1描述重掺杂注入区，而δ2描述非注入衬底。和在均匀衬底时所做的不同[参看式(4.4.33)和有关的讨论]，在这里我们不能为了与实验结果取得最佳一致而完全自由地选择δ参数；我们的选择受到ID及其导数必须是连续的限制。因此不能期望在所有情况下，上述简单模型都能很好地与测量结果一致。然而，为了对正在讨论的器件说明其I-V特性的一些重要方面，我们还将需要上述模型的简单性。有兴趣的读者可能想对这个简单模型用经验的方法加以改进。

和以前一样，在饱和区可以使用式(6.2.33)，其中V´DB确定为当非饱和公式给出dlDN/dVDB=0时的VDB值。如果VSB<VI，并且夹断出现在V´DB<VI时，则利用式(6.2.35a)

和(6.2.36)，可得

可是，如果上式预计的V´DB大于VI，则应该认识到此时夹断点位于注入区之外，因此应当使用式(6.2.35c)和(6.2.36)，并得到

最后，如果VI<VSB<VDB，则可用式(6.2.35b)和(6.2.36)，求得

 完整的强反型模型还是用式(6.2.34)给出，不过IDN和V´DB的表达式要按上面解释的那样来选择。

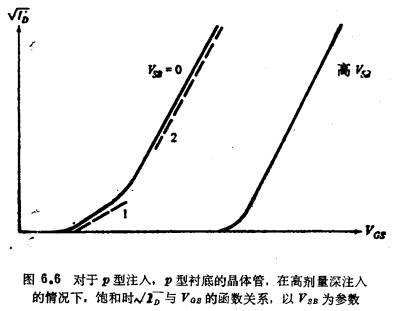
为简单起见，有时用4.4.2节中的非注入沟道近似模型代替上述模型。在这种情况下，我们规定参数δ、VFB、ΦB和γ都是单一的“折衷”值。当注入剂量较低时，这样一种方法可以给出满意的结果。但是，当注入剂量较高时，它的结果是不精确的。图6.6是高剂量注入器件的与VGS的关系曲线(此图与图4.29形成对照)。这种特性无法用4.4.3节中的模型预测，但是可以解释如下：首先假定VSB=0。当VGS较低时，V´DS。也较低，且V´DB<VI。若饱和电流为I´D，则利用式(6.2.33)，(6.2.35a)，(6.2.36)和(6.2.39)，可以求得

式(6.2.43)如图6.6中的虚线2所示。注意，式（6.2.43）中的VGS的截距比式(6.2.42)中的大，斜率也是前者大于后者，这是因为上面提到过的δ2<δ1的缘故。如图中所示，一个真实器件的曲线，当VGS较低时，接近于曲线1，当VGS较高时，接近于曲线2，最后，当VSB>VI时，式(6.2.33)，(6.2.35b)和(6.2.41)给出

式(6.2.44)如图6.6中右边那条实线的直线部分所示(底部的弯曲部分是由中反型和弱反型引起的)。在这种情况下，预测斜率只有单一的值(当然假定迁移率与VGS无关)。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助