解析与衬底同型的注入强反型漏端电流模型

对于图6.10所示的连接方式，非饱和区的漏端电流可以据根式(4.4.13)确定，现将该式重写于下：

    暂且假定μ为常数。[迁移率对栅电场的依赖性可以用有效迁移率方法来考虑(4.8节)。根据这个假定，并利用式(6.2.21)的Q´I，式(6.2.24)变成

    假设VDB>VSB(VDS>0)，我们分三种情况来说明漏端电流：

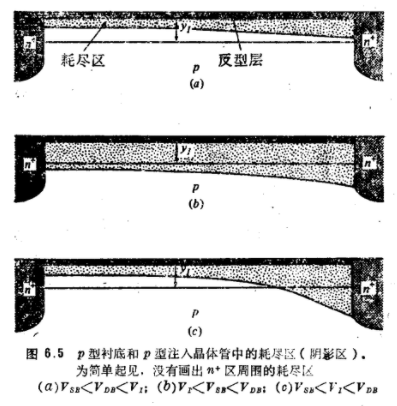
1、VSB<VDB≤VI。如果忽略十分靠近源和漏处的边缘效应，则在这种情况下，沿整个沟道长度，耗尽区都位于阶梯近似的注入区之内(图6.5)。把式(6.2.22a)和(6.2.6)代入式(6.2.25)，给出

    为使后面的公式表示在形式上紧凑一些，我们采用了这样一种表示法：

    这个方程式具有式(4.4.8b)的形式。

2、VI≤VSB<VDB。这时，在整个沟道长度上，耗尽区的边位于阶梯近似注入区之外(图6.5b)。于是，把式(6.2.22b)手口(6.2.15)代入式(6.2.25)可得

    式中I2由式(6.2.27)=2给出。

3、VSB<VI<VDB。这种情况下，耗尽区的边在源附近位于注入区之内，在漏附近位于注入区之外，(图6.5c)。正是在深度力I处的某一点，反型层的反偏电压VCB等于VI。

    因此，式(6.2.25)可写成如下形式：

把式（6.2.6）代入第一个积分，把式（6.2.15）代入第二个积分，我们得到

    其中Ii由式(6.2.27)=1，2给出。

    饱和区的开始点可用第4章中那样的方法来获得，也就是ID与漏端电压关系曲线的斜率变为零的那一点。因为我们目前所用的电压是相对于衬底的，所以这个开始点定义为V´DB=V´DS+VSB。如果当V´DB<VI时出现夹断现象!  则通过令式(6.2.26)的斜率等于零，便有

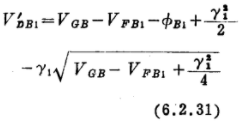
    如果当VDB在大于VI的某一值时出现夹断现象，则令式(6.2.28)或(6.2.30)的斜率等于零，可求得

    如果VSB>VI，显然必须用式(6.2.32)来确定V´DB。假定VSB<VI，如果对于给定的VGB，式(6.2.31)所预计的V´DB值小于VI，则将用该式来确定V´DB。可是，如果式(6.2.31)所预计的V´DB的值大于VI，则这个值应该舍去，并改用式(6.2.32)，因为在那种情况下，出现夹断时，沟道源端附近耗尽区的边位于注入区之外。如果沟道长度调制效应可以忽略，则通过在式(6.2.26)，(6.2.28)和(6.2.30)的其中之一适当方程中用证确的V´DB代替VDB就可得到饱和电流：

    包括非饱和区及饱和区的完整模型为：

离子注入器件中的沟道长度调制效应尚未得到很好地描述。因此经常使用非注入器件的模型(5.2节)，不过对其中的参数用经验方法加以调整。

    注入器件的ID-VDS特性的一般形状与非注入器件的特性相似，  但也确字存在一些特点。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助