MOS晶体管组合几种效应于一个模型之中分析

迄今今我们已经讨论了各种效应，为简单起见，每次只考虑一种。但是，在一个实际的器件模型中，必须同时考虑若干个这种效应。为了恰当地做到这一点，必须研究这些效应之间的相互作用，但遗憾的是，这样所得的表达式将变得十分复杂。如果每种效应独自的影响较小，则经常采用的一种经验方法是假设这些效应之间无相互作用。举例来说，考虑一个沟道底短又窄的器件。为了获得正确结果，这里需要用三维分析。然而，如果只是为了粗略地估算，对于这样一个器件，有时可利用有效阈值电压公式来建立模型，有效阈值电压等于TT-∆VT-∆VT1，其中VT为长沟道阀值电压，∆VT为假设只存在短沟道效应时的阈值电压的减少量，∆VT1为假设只存在窄沟道效应时阈值电压的增加量。当∆VT和∆VT1较小时，可以证明，这种方法在某种程度上是正确的。

例5.4基于上述无相互作用的假设，作为一个建模的例子，下面我们设法来推导一个包括下列各种效应的漏端电流表达式：

1.L对有效阈值电压的影响

2.VDS对有效阈值电压的影响

3.W对有效阈值电压的影响

4.速度饱和效应

5.有效迁移率与垂直电场的相关性

6.饱和区的沟道长度调制。

这里所用的方法将是文献中所用方法的一个变种。前三项影响将用下面的有效阈值电压来模拟（参看前面的讨论）：

式中的∆VT（L，VDS）和∆VT1（W）可按5.4节中所说的方法计算。第四种效应可像例5.2（5.3节）那样来模拟，第五种效应可利用式（4.8.18）来计入[参看式（5.3.11）下面的讨论]。

这样，在非饱和区有：

式中（VDS）由式（5.5.1）给出。

漏-源电压的夹断值VˊDS可用5.3节中已说明的方法求出，即根据式（5.5.2）建立dID/dVDS=0的方程，并在计算中忽略VT与VDS的相关性。这样重又导出式（5.3.12）。通过更精确的计算可导出相当复杂的表达式，但所给出的值实际上仍与式（5.3.12）一样。

现在我们将确定饱和区的ID。这里需谨慎一些。如果像在5.2节中那样隐式地假定，与VDS无关，则我们可以采用式（5.2.5），其中的IˊD可由式（5.5.2）给出，此时式（5.5.2）中VDS要用VˊDS来代替。在最后的IˊD式中，VDS本身将不出现。情况当然应该是这样的，因为不管VDS的实际值是多少，被认为已夹断的沟道末端的电势（相对于源）总是假定为VˊDS。然而，正如式（5.5.1）已显式地指出的那样，我们在这里仍需计入VDS对的影响。前面已经指出过，这一效应假定与夹断无关，不论VDS是大于或者小于VˊDS，它都存在，因为甚至当VDS>VˊDS时，沟道区也直接受到来自漏附近场强线的影响。因此，即使在饱和区，也将继续是VDS，而不是VˊDS的函数。从而有

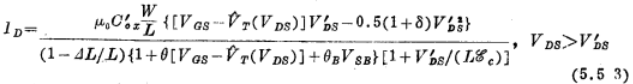
其中∆L/L用式（5.2.6）给出。这时，可能有人会提出异议，认为在分母的最后一个因式中应该用L-∆L，而不是L。然而，在当前这种经验建模的水平上，不值得这样考虑，因为两者的差别很小。最后，为了使ID（VDS）的斜率在VDS=VˊDS处连续，还将需要对VˊDS值略作修正，这已在5.2节中解释过了。

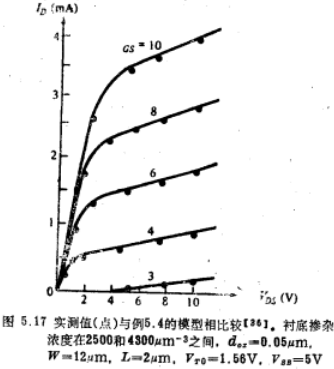
采用θB=0的上述模型已在别处提出，并与实验结果进行了比较，如图5.17所示。不过，由于4.8节中所讨论的原因，我们宁可考虑θB不等于零。

如在本节中所见，文献中大多利用有效阈值电压来研究短沟道和窄沟道效应。因此，显式地包含阈值电压的近似模型（4.4.30）式显然是较有用的。与此相反，精确模型（4.4.8）式没有显式地包含阈值电压，因而本节中的一些结果不能直接与它结合使用。这就使得近似模型被广泛地用于小器件。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助