四端MOS结构通用电荷薄层模型解析

在本节中，我们要推导一个适用于所有工作区的漏端电流表达式。标题中的通用二字就是对这一广泛适用性而言的。电荷薄层这一术语是指这一模型中的基本假设，即反型层具有无限小的厚度^①。因为注意到在第2和第3章中已经作了这一假设，所以可把第2、3章中的表达式用到现在的推导中来。下面我们将要介绍的这种模型已在若干参考文献^{[53，54,56-59]}中导出，但是我们的推导方法将更简单。

要使我们将要导出的结果具有通用性，其关键是承认沟道中的电流可由漂移和扩散（1.3节）两种机制引起这一事实。这样，令x为沟道中沿水平方向从源端测量的位置。如果x处的反型层电流记作I（x），则有

为了写出漂移分量的表达式，现在来考虑图4.2a中在反型层内x和x+Δx之间的一个小单元，该小单元被放大示于图4.4中。这一单元两端的电势差的Δψs（x）=ψs（x+Δx）-ψ（x）。把图4.4与图1.5相比较［假设电子速度正比于微小的水平场强，与式（1.3.8）类似］，显然可以采用式（1.3.15），但需把V用Δψs来代替，a用Δx，b用W来代替，|Q´|用一|Q´I|来代替，这里的Q´I是x处的（负的）单位面积反型层电荷。μ_B也必须用一个较小的迁移率值来代替，因为电子平行于表面（半导体-氧化层界面）运动时，会被垂直方向的电场拉向表面，故运动困难。

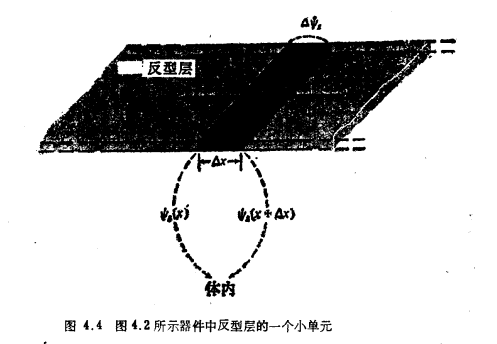
对应的迁移率称为表面迁移率，记为μ（此量将在4.8节中更详细地加以考虑，现在可粗略地假定为μ_B的一半）。这样便有

令Δx趋近于零，该式便成为

仿照式（1.3.20）可得扩散电流分量：

此处应注意，若假定反型层具有有限厚度，且其中的电子浓度随深度而变，则只要假设电子电流是“层流”，式（4.3.3）和（4.3.4）将仍然适用。这是由于式（1.3.15）和（1.3.20）具有普遍性，这种普遍性已在1.3节相应的脚注中讨论过了。然而，这一点在这里并不十分重要，因为在这里假定所有反型层电荷都集中在离“表面”无限小的深度范围内。

在直流稳态下（本章只讨论这种情况），沟道中的总电流在所有x处都必然相同且等于漏端电流。计及这一事实，并把式（4.3.3）和（4.3.4）代入（4.3.1）可得

把沟道源端处（x=0）的表面势记作ψso，该处的Q´I记为Q´I,表画。把沟道漏端处（x=L）的相应量记为ψsL和Q´I,栅。然后把式（4.3.5）从x=0到x=L积分，可得

由于ID与x无关，故可移到积分符号之外，因此等号左边等于IDL，从而有

这样，我们可把ID看成由两个分量ID1和ID2组成^[52，63]，

其中ID1由漂移引起

由扩散引起

对ID1和ID2的解释要小心谨慎。注意，由于式（4.3.3）中的I漂移（x）和式（4.3.4）中的I扩散（x）是位置的函数，故一般说来，沟道中的漂移电流和扩散电流可能不是单一值^[65]。然而，导出式（4.3.7）的推导过程清楚地表明，之所以有ID1，是因为假定沟道中存在漂移；如果没有漂移，也就没有ID1。同样，之所以有ID2，是因为假定沟道中存在扩散。

现在假定沿沟道μ以为常数（更一般的情况将在4.8节中讨论），于是，μ可移到式（4.3.9）和（4.3.10）中的积分号之外，故得到

为了计算ID1和ID2，我们需知Q´I与ψs的函数关系。前面已经导出过一个合适的表达式，即式（3.2.8a），现重写于下。[当然，假定式（3.2.8a）在这里是适用的，因为在本章开头就作了“缓变沟道近似”。]

根据式（3.2.5b），上式中的Q´B为

因此，Q´I可写成

把上式代入式（4.3.11），便给出由漂移引起的漏端电流分量：

把式（4.3.15）代入式（4.3.12），可给出由扩散引起的漏端电流分量：

现在只剩下根据图4.2a中的外加电压来计算ψso和ψsL这一步了。把图4.2a与图3.1c相比较，我们注意到，为后者导出的表达式可以用于沟道的源端，只要用VsB去代替VCB即可，同样，用VDB去代替VCB这种表达式也可用于沟道的漏端。因此，对沟道的源端和漏端写出式（3.2.7b），便得［53-59]

这些方程可用迭代法对ψso和ψSL求解。这种求解不难用计算机或具有解方程功能的计算器来完成^①。ψSL与VDB（或ψSO与ψSB）的关系曲线示于图4.5。图中所使用的符号已在第3章中定义过。标有数字的一些点与将要进行的讨论有关。

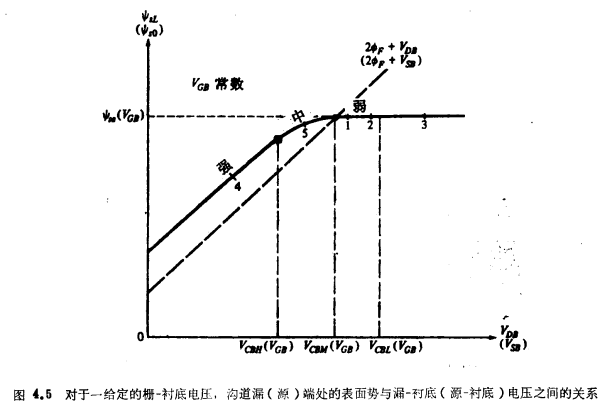
注意，由于忽略了漏附近的边缘效应，结果沟道漏端处的表面势为ψSL，一般情况下，它与n⁺区的电势是不同的。这样，在n⁺区的边界上，电势似乎是不连续的。根据3.2节中近末尾处的讨论可以预料，较详细的描述应该计及包含边界的过渡区，在这一过渡区上，电势连续地变化，并最终等于n⁺区的电势。可以预计，过渡区的长度粗略地等于漏下面耗尽区的深度，在这一过渡区中，不能再假设电场实际上是垂直的。对于沟道源端也可采用类似的论述。基于这样一种描述，在上面的分析中，可以把I解释为除去源、漏过渡区后的沟道长度，而ψSO和ψSL分别表示源端过渡区之右和漏端过渡区之左的表面势。于是，再假设VSB和VDB在两点处的作用基本上相同^②，则又可以应用式（4.3.18）了。然而，对于本章中所假设的长沟道，我们可以继续把工看成源漏之间的总距离。注意，为了能获得简单的解析结果，我们采纳了“缓变沟道近似”，而这种近似不能处理上述边缘效应，这样就迫使我们在分析中忽略边缘效应。仔细研究上述效应需要采用二维数值分析。

现在固定VSB，保持VGB为一参数，并变化VDB，于是从式（4.3.18）可求出相应的ψso和中ψsL，并把它们代入式（4.3.16）和（4.3.17）。然后把求得的ID1和ID2按式（4.3.8）那样加起来而求出ID，并绘成图4.3a中的曲线，该图中的电流对应于VDB>VSB，以VGB为参数。这些曲线可以转换成图4.3b中的曲线，该图中的曲线表示了电流与VDS=VDB-VSB的关系，以VGS=VGB-VSB为参数。在两张图上，按表4.1标出了工作区，并用了第3章中所定义的符号表示出了VGB或VGS的界限值。在这里这些值没有多大意义。重要的是单个表达式（4.3.8）能预测所有工作区中的电流，而且还能与实验结果吻合得很好^[55-59]。

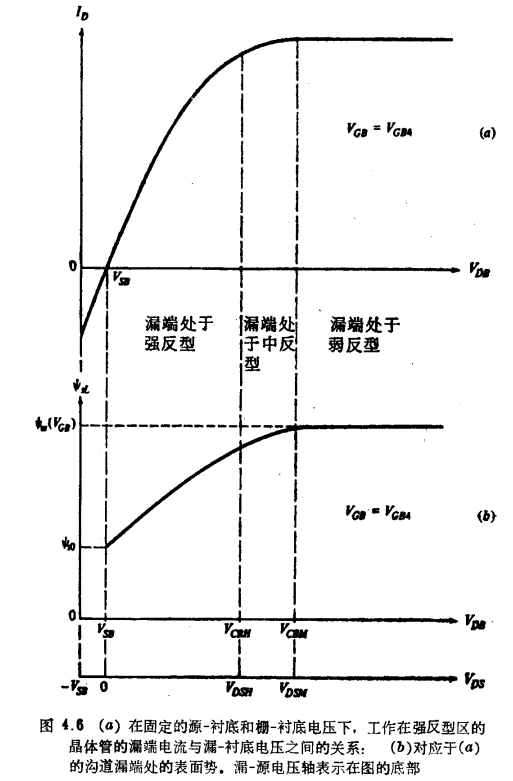
注意，对于较大的VDB值，所有曲线最终都会饱和。从对应于某一VGB值（比如说VGB4）的漏端电流与漏端处相应的表面势之间的关系，便可理解这一点，现用图4.6来说明。如图所见，增加VDB最终将驱使沟道的漏端进入弱反型，由于第3章中已说明的原因，此时ψSL工实际上变为只取决于VGB=VGB4的常数了。进一步增加VDB再也不能影响ψSL。因而式（4.3.16）和（4.3.17）中的ID1和ID2也变得与VDB无关了。于是可以看出，虽然沟道的源端，比如说，处于强反型，并有很大的|Q´I|，同时ψsO也强烈地依赖于VSB，但是沟道的漏端却处于弱反型，且|Q´I|很小，以及ψsO实际上与VDB无关。不过在沟道的两末端处（以及在整个沟道中）电流是相同的。对于这一结论不应感到惊奇，因为据式（4.3.5）可知，在沟道任意一点上的电流并非只由Q´I确定，这一点将在今后进一步予以讨论。

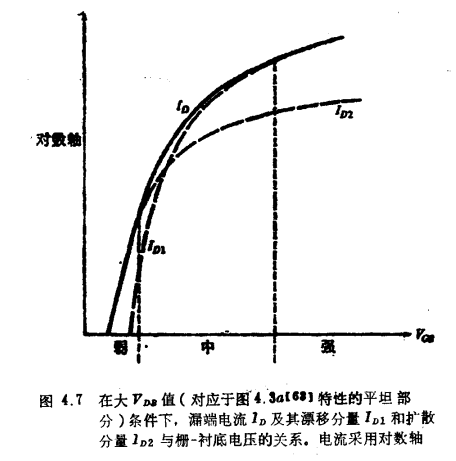
现在来考虑图4.3a中曲线“平坦”部分的一个VDB值。固定这个VDB值，绘出ID及其分量与VGB的关系，则得到图4.7的曲线^［53 ]。为了使曲线包括的电流值范围能大些，故纵轴采用对数轴，在横轴上已按表4.1的定义标出了反型区。这里因为VDB大于VsB，因此反型最强的沟道末端是与源相邻的一端。这端处的反型情况可象第3章那样确定。这里我们指出一点，在晶体管文献中，弱反型往往没有下限，也就是说，凡是在中反型之下的都算弱反型，只要电流不小到被漏电电流所掩盖就可以了（见4.6节）。

在图4.7中可见，强反型区内，ID≈ID1，因此电流主要由漂移引起。在弱反型区内，由于ID≈ID2，故电流主要由扩散引起。然而在中反型区内，ID1和ID2两者都重要，也就是说，在这一区内漂移和扩散都起着重要的作用。对于其余的VDB值也有类似的结论。

现在我们来讨论在弱反型区（此时ID～ID2）与式（4.3.17）有关的数值问题。考虑工作在这一区域的一个晶体管，比如说其VSB和VDB分别对应于图4.5中的点1和点2。如图所见，此时ψSL近似等于ψSO（在图中看不出差别）。这样，即使是ψSL和ψSO值的一个很小的误差也会造成差值ψSL-ψSO的一个大的相对误差，而这一差值正是式（4.3.17）所依赖的基本因式。因此在电流中所产生的相对误差也可能较大。于是，只有在特别精确地已知ψSL和ψSO时，才有希望从式（4.3.17）求得ID，求解式（4.3.18）以得到ψSO和ψSL需要经过几次迭代。这说明在弱反型区，式（4.3.17）中的。不能采用近似的显式表达式。在题4.2中提供了克服这一缺点的方法。

从式（4.3.8），（4.3.16）和（4.3.17）清楚可见，ID可写成如下形式：

其中

式（4.3.19）是强调晶体管对称性的一种形式。如果源和漏处的电势互换，则唯一的差别是ID改变正负号。式（4.3.19）形式的ID表达式也可以从式（4.3.7）直接导出。事实上，如果f（ψs）具有一个合适的函数形式，甚至当μ取决于ψs时，式（4.3.19）也适用。

对已经介绍过的通用电荷薄层模型，文献中经常用准费米势（附录I）概念来推导。这将使推导过程较我们的推导更为复杂^{[53,54,56-59]}。不采用电荷薄层近似，而允许反型层向表面以下伸展，甚至允许在耗尽区内还存在空穴，这样进行电流计算也是可能的；包（Pao）和萨（Sah）很早就这样做了^［10］（附录I）。虽然他们的分析被认为是十分通用和精确的，但由于它包含了重积分的数值计算，因此计算效率低。最近已有人提出重积分公式可以简化为等效的单积分公式^［62］，但仍要求数值积分。我们所介绍的电荷薄层模型与这些通用公式之间吻合得极好^［62］，且不要求数值积分。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助