三端MOS结构弱反型特性函数形式现象分析

对于一给定的VCB值，弱反型区定义为（图3.2）：

在这一区内，有

现在来考虑式（3.2.6）。该式中第一个根号下的第二项的值是不大的，这是因为在弱反型区，ψs<ΦM然（图3.2），并且从式（3.4.2）可知，ΦM=2ΦF+VCB。因此，和导出二端结构的式（2.5.33）一样，可以用泰勒级数展开求得Q´I：

我们要提醒读者，在弱反型区内，VCB不能解释为有效反向偏压，这在3.3节中已经解释过。在弱反型区，表面势实际上与VCB无关，而是等于ψsa（见图3.3）。ψsa的表达式由式（3.2.16）给出，因此有

因而，在式（3.4.28）中，只有θxp（-VCB/Φt）项与VCB有关。为了强调这一重要结论，可把式（3.4.28）写为如下形式：

对于弱反型区内的任意VGB值，ψsa可从式（3.4.29）确定，并把它代入式（3.4.30）以求得Q´I。对于一个固定的VCB值，Q´I（VGB）结果为指数关系。为了说明这一点，现在像对二端结构所做的那样，来推导一个不包含ψsa的Q´I表达式。在图3.7中，我们重画了一条图3.3中的曲线。令Q´CB表示获得这条曲线所对应的常数值VCB。在图上标出了用表面势ψs表示的弱反型区的两个界限点，该两点上的表面势值可从式（3.4.1）和（3.4.2）求得。可见，用ψs表示的弱反型区的宽度只有ΦF。随着VGB在这一区中变化，式（3.4.28）中项的相应变化与该式中指数项的急剧变化相比是很小的。因此，可假定实际上固定在值上，而1.5ΦF+V´CB即为弱反型区中点（图3.7中的x点）上的ψs值^[10]。这样，式（3.4.28）变成为

图3.7中曲线的斜率在弱反型区近似为常数，且可近似等于该区中点处的斜率值。根据式（3.4.29），中点处斜率的倒数（通常用n表示，但不要与电子浓度相混淆）为

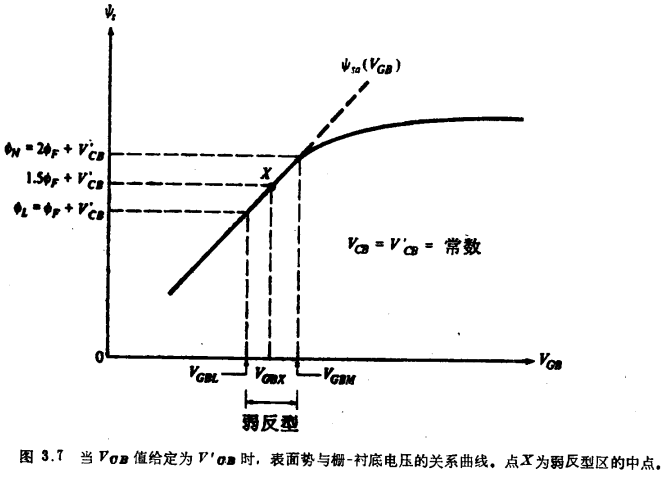
因此，在弱反型区，VGB改变ΔVGB将引起ψs改变Δψs，并有Δψs=ΔVGB/n。我们将相对于弱反型区的中点来取上述两个变化量，已知在中点（图3.7中的Χ）上ψs=1.5ΦF+VC´B，相应的VGB值可从式（3.4.29）求得：

于是式Δψs=ΔVGB/n可写成如下形式：

其中

把式（3.4.34）代入式（3.4.31），可得

其中Q´IX为弱反型中点上的Q´I值，用下式给出

若VCB固定不变，而VGB变化，则式（3.4.36a）是一个十分有用的方程式，因为该式使Q´I与VGB的指数关系成为显式的。然而，若VGB固定不变而VCB变化，则式（3.4.36a）将使人迷惑不解，原因是该式难以预测Q´I与VcB的关系。Q´IX，n和VGBx中隐含着VCB，并以一种复杂的方式依赖着它。另一方面，由于式（3.4.30）使Q´I与VCB的指数关系成为显式而又十分简单，故该式是VGB固定而VCB变化的这种情况下的理想公式。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助