关于二端MOS结构中反型界限的精确定义分析

关于反型界限的精确定义分析

在2.5节中，中反型区的下限点取得和弱反型区的上限点重合。而弱反型区的上限点传统上定义在ψs=2ΦF。如从式（2.4.11b）可见，当ψs=2ΦF时，表面电子浓度变得和体内的排杂浓度NA相等。从式（2.6.14）和（2.6.15）还可看出，此时C´i=C´b。以上两个论点的成立与C´ox值无关。然而，两个论点都没有提到在ψs=2ΦF时，常用的“弱反型近似”［如Q´I（VGB）是指数形式]是否仍有效，这是因为不涉及C´ox值就无法仔细讨论这种近似的有效性。因此，具有实际意义的做法是，把C´ox考虑进去，并重新定义某一点为中反型区的起点，超过这一点，常用的弱反型近似不再适用。在弱反型区内C´i可以忽略的那些点上（图2.15），C´b变化很小；因此，式（2.6.18）中的dψs/dVGB近似为常数。这是与VGB成指数关系所必需的，这一点可从由式（2.5.37）到式（2.5.43）的推导过程中看出。如果式（2.6.18）中的C´i与C´ox+C´b相比开始变得显著起来，则这样一种特性将会有明显的偏离。这样，让我们定义中反型的开始点为^［14］：令该点的ψs和VGB值分别为中ΦMO和VMO，即

在这一点上，有

记住，由于C´b变化较慢，故不难看出，在图2.9中，曲线在该点处的斜率dψs/dVGB降低到约为弱反型底部斜率的91%。In｜Q´I｜~VGB曲线（图2.11）的斜率也以同样比例下降，这个斜率是Q´I（VGB）的“指数特性”的一种度量）。

为了精确求出中ΦMO的值，需要把式（2.6.14）和（2.6.15）代入式（2.7.1），并选代求解ψs于是相应的VMO便可从式（2.5.18）求得。所得结果取决于氧化层厚度和衬底掺杂。可以证明，当这些参数是常用的实际值时，前面所定义的ΦMO加o值与式（2.5.9）所给出的2ΦF值之间的差别约不大于多数实际情况，为了简单起见，我们可以继续使用式（2.5.9）和（2.5.1）。

现在我们转向讨论中反型区的上限点。具有实际意义的做法是，把中反型的上限点定义在这样一个点上，低于该点，常用的强反型近似，即式（2.5.28）不再适用。我们再来看一下式（2.6.20）给出的Q´I（VGB）曲线的斜率。在强反型区的预部，C´i很大，式（2.6.20）将简化为d｜Q´I｜/dvGB≈C´ox;当然这一点与式（2.5.28）是一致的。如果C´i比C´ox+C´b大得不多，则d｜Q´I｜/dvGB将小于C´ox，式（2.5.28）也将不成立。于是，让我们定义中反型区的上限点如下^［14］：

令该点的ψs和VGB值分别为中ΦHO和VHO，即

在这一点有

从式（2.6.20）不难看出，在这一点上，｜Q´I｜与VGB关系曲线的斜率（图2.10）将减小到约为它的理论最大值C´ox的91%，同时从式（2.6.18）可看出，此时ψs（VGB）曲线（图2.9）的斜率将下降到约为其最大值的9%。

为了求出ΦHO值，必须把式（2.6.14）和（2.6.15）代入式（2.7.2），并代求解ψs。我们求得中加ΦHO比中ΦMO大几个Φt（大约为6Φt），其精确值与氧化层厚度和衬底指杂有关。若中ΦMO精确地已知，则可用它代入式（2.5.18）而求得VHO。（注意，ΦHO的小误差将导致VHO的大误差，因为公式中存在指数项，而现在指数项又比较大）。

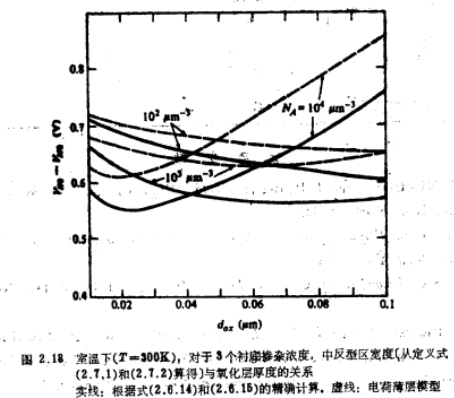
对于各种工艺参数，VHO-VMO的值在图2.18中用实线表示。在这一计算中。我们使用了定义式（2.7.1）和（2.7.2）以及精确的电容公式（2.6.14）和（2.6.15）。电荷薄层模型预计的VHO-VMO比较大，如虚线所示。这是由于该模型不能精确预计C´b的缘故（图2.15）。在图2.18中可见，中反型区的宽度随工艺参数而显著变化。然而，并非氧化层厚度和衬底掺杂的所有组合方案都是在实际中采用的。例如，在MOS晶体管制造中，大的掺杂浓度通常与薄的氧化层相组合。因此，对于各种实际情况，中反型区的宽度相差并不很大。在室温下，它的平均值约为0.6V。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助