二端 MOS结构反型的一般关系式解析

反型的一般关系式

对于掺杂浓度取MOS晶体管中常用值（10²~10⁵μm^-3）的衬底，费米势ΦF的值近似为9Φt~16Φt；因此，式（2.4.17）中的2Φt为18Φt~32Φt。不难看出，在反型区图2.5c），因为ψs≥Φt，式（2.4.17）可以近似写成下式①：

氧化层下面的总电荷（单位面积上的）是来源于反型层中的电子电荷Q´_I和来源于耗尽区中电离受主的电荷Q´_B之和：

现在我们来估算Q´_I和Q´_B。首先考虑在反型层中的电子。在图2.5c中，坐标是的任意一点上的电子浓度由式（2.4.13）给定。

当沿轴离开表面时，由ψ_s降低到零，并且由于与中成指数关系，故急剧衰减。因而，我们可以选择一点，使在该点以下，电子浓度可以忽略。于是，所有自由电子实际上包含在和之间的一层空间内（图2.5c）。中心在，厚度为且平行于表面的薄层中所包含的自由电子数为，其中A为顶视截面积。这些电子的总电荷是。于是我们可把反型层中所有电子的电荷Q_I用下式表示：

这样，单位面积反型层电荷Qf将由下式给出：

用这种方法来求Q´_I的值需要较长的计算过程，并且要用数值积分方法（附录F）。因此，我们将用一个广泛采用的简化方法来代替它：先确定一个足够精确的Q´ _B名的表达式，然后再返回去根据式（2.5.2）和（2.5.1）来求Q´_I的值。下面我们先集中注意力于耗尽区。和pn结中的情况一样，我们认为耗尽区具有明显边界，其深度在表面之下ι_B处（图2.5c），反型层就在耗尽区的顶部。数值计算结果（附录F）表明，反型层中的大部分电荷集中在非常靠近表面处（百分之几微米以内）。由于耗尽区的深度ι_B通常要大得多，因此可以认为反型层是一厚度可以忽略的薄层^[5-10]，称为电荷薄层近似^[8]，这意味着实际上全部耗尽区内没有电子。由于忽略了厚度，因而反型层两端的电势降落也将被忽略，于是，我们假设全部表面势。降落在p型讨底的耗尽区上。因此可以把ι_B与ψ_s用和1.5节中分析n⁺p时的类似方法联系起来。再假设在耗尽区内可动载流子浓度与电离受主浓度相比可以忽略，在1.5节中已把这种假设称为耗尽近似。在这种假设下求解泊松方程（1.2.13），可导出一个类似于式（1.5.13）的方程：

令Q´_B为耗尽区内电离受主的单位面积电荷，对应于式（1.5.14）有：

把式（2.5.6）和（2.5.1）代入式（2.5.2），最后可得单位面积反型层电荷^①：

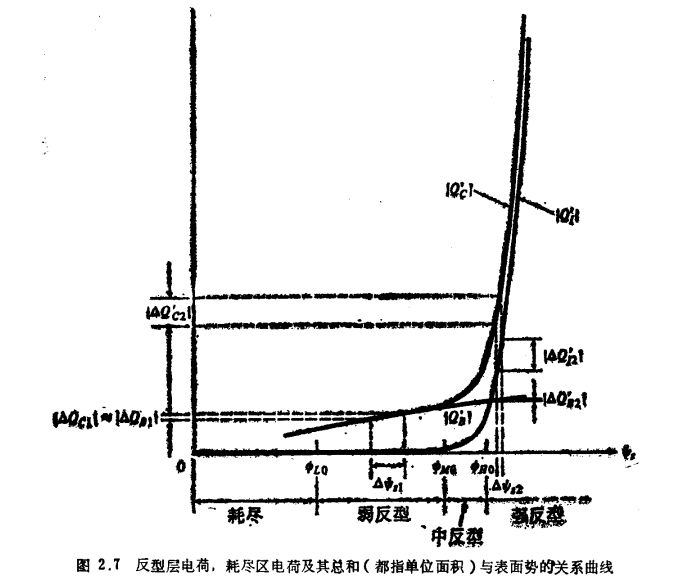
利用式（2.5.6）和（2.5.7），我们在图2.7中绘出了｜Q´_B｜，｜Q´_I｜以及它们之总和｜Q´_c｜与ψ_s的关系曲线。

一种方便的做法是把反型区分为三个子区：即在图2.7中被称为弱反型、中反型和强反型的三个区。为了和图2.6中的反型定义相一致，可把图2.7中的弱反型的开始点定义为

弱反型区的上限点在很多文献中定义为

从图可见，当表面势小于此值时，实际上几乎全部表面电荷来源于耗尽区电荷，相应的反型层电荷因太小以致在图2.7的标度下难以表示出来。然而，当MOS结构是晶体管的一部分时，这些极少量的反型层电荷却可以产生不可忽视的导电能力。随着s增加到高于2Φ_F，由于式（2.5.7）中存在指数项，｜Q´_I｜开始显著地增大。当ψ_s超过2ΦF几个Φt时，｜Q´_I｜变得强烈地随ψ_s而变化。对于这一结论，不应感到奇怪。从图2.6可见，在中ψ_s=2ΦF处，表面电子浓度已经和受主离子浓度一样高了。由于式（2.4.12）表明n表面属与ψ_s是指数关系，所以中ψ_s在2ΦF之上再增加几个Φt后就足以提供很大的n表面在紧靠表面的各点上的浓度也将急剧地增加，从式（2.5.4）可见，｜Q´_I｜值将开始“起飞”了。我们可以在此附近取一点，定义为强反型的开始点，图2.7中用ΦHO表示。即有

式中ΦzO等于几个Φt。把强反型定义得更明确些，即把ΦzO的值取得更确定些是可能的，对此有兴趣的读者可参看2.7节。

除了Q´_I和Q´_B对Q´_C的相对贡献外，讨论一下由于表面势改变ΔQ´_I而引起的电荷改变量对ΔQ´c的相对贡献也是十分重要的。ΔQ´c的一部分由反型层电荷的改变量ΔQ´_I提供，另一部分由耗尽区电荷的改变量ΔQ´_B提供，即从式（2.5.2）可见，有

首先考虑低VGB，因而也是ψs和｜Q´_C｜较小的情况。假设VGB改变ΔVGB1引起电荷变化ΔQ´c1，如图2.7所示。从该图可清楚地看到，这一电荷的改变量实际上全部由耗尽区的电荷改变量ΔQ´_I提供。而且，为供应这些电荷变化量所要求的表面势的变化量Δψs是相当大的。显然，刚才所描述的现象是图2.7中标出的“弱反型”区（除了十分靠近该区上限的一些点外）的主要特征。

现在假设VGB较大，它所引起的ψs和｜Q´_C｜也较大。假设VGB改变ΔVGB2引起电荷变化ΔQ´c，如图2.7所示。与前面所述情况不同，现在实际上全部ΔQ´c（应为ΔQ´c2——译者）由反型层电荷的变化量ΔQ´_I2所提供，而ΔQ´_B（应为ΔQ´_B2——译者）可忽略，且引起这些电荷改变量所要求表面势的改变量Δψs2很小。在图2.7中标有“强反型”的整个区域内都明显具有这一特性。

让我们稍停片刻，以便总结一下在推论中得到的一些最重要的结果。我们已经导出了足够的用于表征MOS系统反型特性的方程，这些方程是：

1、电势平衡

式（2.3.1）是电势平衡方程，为方便起见，重写如下：

2、电荷平衡

根据式（2.3.3）和式（2.5.5），有

3、电荷与电势的关系

下面3个方程式把每一电荷变量和与其有关的电势联系起来。具体说来，栅上的电荷通过式（2.4.18）和加在氧化层两端的电势差相联系，重写如下：

反型层电荷用式（2.5.7）与表面势相联系，有如下形式：

最后，耗尽区电荷用式（2.5.6）与该区两端的电势差相联系，有如下形式：

式（2.5.12）至式（2.5.16）5个方程包含了6个变量，其中3个是电势差（V_GB，ψ_ox，ψ_s），3个是单位面积电荷（Q´_G，Q´_I，Q´_B）。在5个方程中，我们可以消去6个变量中的4个，从而导出其余2个变量之间的关系式。例如，让我们来推导VGB和ψ_s之间的关系式。消去另外4个变量，可得

或者再用式（2.5.2）和（2.5.1）导得

式中

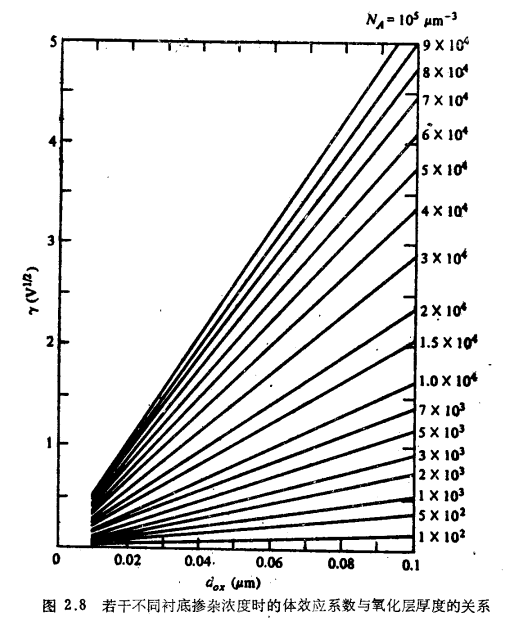
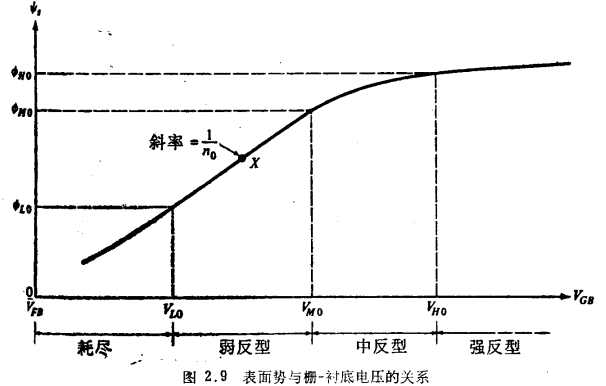
适合于各种工艺参数的γ值示于图2.8中。参数γ称为体效应系数（其原因在第3章中将显而易见）。式（2.5.18）绘于图2.9，在该图中以ψ_s与V_GB的关系表示出来（虽然该方程式不可能对ψ_s有显式解）。注意，对于曲线上较低部位的一些点，为提供因ΔVGB所引起的电荷变化量要求有较大的的Δψ_s（也与图2.7有关）。而对于曲线上较高部位的一些点，只要一个微小的Δψ_s就足以提供这些电荷变化量，这是由于图2.7中曲线的陡度所造成的。弱反型区的特征是斜率dψ_s/dVGB较大，且近似为常数；而在强反型区内，这一斜率降低到很小值。

若用VGB来表示，则弱反型、中反型和强反型的开始点将分别记为VLO、VMO、和VHO^.如图2.9所示。VLO和VHO可以从式（2.5.18）求得，只要令其中的ψ_s分别等于式（2.5.8）中的ΦLO和式（2.5.9）中的ΦMO。然后忽略式（2.5.18）中较小的指数项，可得

为了求得VHO，可令式（2.5.18）中的ψ_s=ΦHO，只要ΦHO已准确的知道。注意，因为ΦHO如式（2.5.10）所指出的要比2ΦF大几个Φt，所以这里的指数项不能忽略。因此，即使是ΦHO的一个小误差也会引起指数项的一个大误差，因而也造成ΦHO的一个大误差。通常，可求得

式中VZO为零点几伏（对于实际器件，室温下的典型值是0.6V）。（对VZO值的进一步讨论请见2.5.2节）

在目前的推导过程中，希望找出一个如下形式的关系式：

遗憾的是。如果企图从式（2.5.12）至式（2.5.16）导出这样一个关系式，所得结果只能是一个隐式表达式，即Q´_I不能闭式地表示为VGB的函数。若VGB值给定，Q´_I值待求，那就只能用数值方法求出所得复杂方程的解。

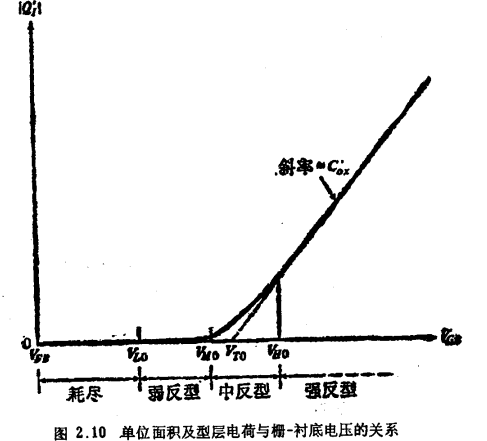
就我们的应用来说，可考虑用参数表示法来代替式（2.5.23），这种参数表示法由式（2.5.7）和（2.5.18）组成。若设定ψs值，则对应的Q´_I和VGB就能从这两个公式中求得。于是Q´_I与VGB的关系曲线就可绘出，如图2.10所示。

让我们再来推导一种Q´_I的表达式，为以后所用。若在式（2.5.12）至（2.5.14）中消去Q´_G和ψ_ox，然后把式（2.5.6）和（2.2.6）代入结果式中，可

这样，可以把式（2.5.24）和（2.5.18）看成Q´_I和VGB之间关系的另外一种参数表示。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助