半导体二端 MOS管电势平衡和电荷平衡分析

电势平衡和电荷平衡

现在我们来讨论，当假设外加电压VGB不等于平带电压VFB时，衬底将受到怎样的影响。其一般情况示于图2.4，外加一个任意值的电压VGB通常将使半导体内出现电荷。实际上，所有这些电荷将包含在靠近半导体上表面的一个区域内，如图2.4a的阴影区。这个区域以外的衬底实际上是中性的。我们把该区两边总的电势降落（方向选为由表面指向该区以外体内的一点）定义为表而势中ψs。今后我们将特别注意该区域的宽度。

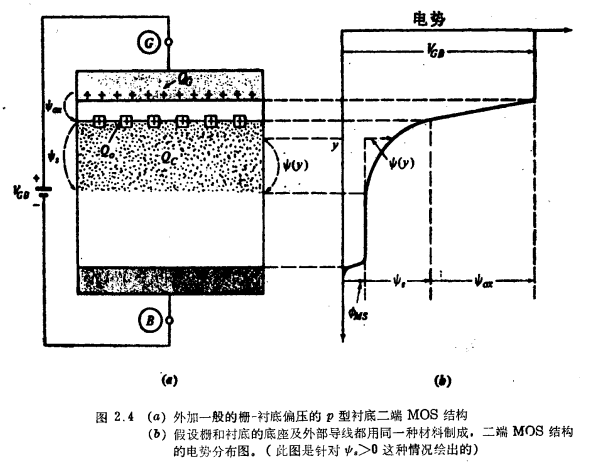
从图2.4可见，在回路中可遇到四种电势降落：

1.外电源的电压VGB。

2.氧化层两边的电势降落中ψ_ox。

3.表面势中ψ_s。

4.若干接触电势。从式（2.2.1）和（2.2.2）可知，沿顺时针方向绕行时，这些电势降落之和为ΦMS。

沿整个回路绕行一周，我们可写出：

对于栅、衬底的接触金属及导线均由同一种材料（例如铝）制成的简单情况，上式所表示的“电势平衡”见图2.4b，在这种情况下，图中所包含的接触电势只有衬底和衬底金属底座之间的接触电势。如果所包括的接触超过一个，则式（2.3.1）仍然成立，但在电势图中应包括所有的接触电势，这些接触电势相加后等于式（2.2.2）给出的值。

注意，式（2.3.1）中的中ΦMS为已知常数，因而VGB的任何变化必定被中ψ_ox和ψ_s的变化所平衡，即

现在来考虑该系统中的电荷。在图2.4中，我们遇到三种电荷：

1.栅上的电荷Q_G。

2.有效界面电荷Q_o。

3.氧化层下面的半导体中的电荷Q_c。

在整体看来是电中性的系统中，这些电荷必须互相平衡。若采用单位面积电荷，则有

从现在起，大部分时间将采用单位面积电荷，而不用电荷，甚至为简单起见，我们常省略“单位面积”这些字，但文中仍暗指是单位面积上的电荷。

注意，如果Q´G发生变化，由于现在假定等效界面电荷Qo是固定不变的，因此Q´c也将有一个变化以达到式（2.3.3）所要求的平衡：

我们已从一般的物理定律出发导出了电势平衡方程（2.3.1）和电荷平衡方程（2.3.3）。我们将会看到，MOS系统特有的一些性质还将使上述方程中出现的各量之间有另外一些的关系式。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助