PN结器件的电流-电压特性及其小信号等效电路

PN结器件

对硅材料的一个区城用型杂质，对相邻区域用p型杂质作选择掺杂可制成一个所谓pn结，这样一个结示于图1.15中。在这图中，我们假设在从n型到p型的边界上，掺杂类型突然改变，且边界两边的掺杂浓度都是均匀的，这样一种结称为突变结或阶跃结。在画图1.15时，我们也已假定n区的掺杂重于p型区。顶部和底部的帽子由选定的金属制成，以实现与半导体的“欧姆接触”（在两个方向上都能良好导电的接触）^①。

①电压表的引出端总是用同种材料制成的。如果把电压表内部电路的各种接触电势都考虑在内，则引出端由两种不同材料制成的这种“学术上”的清况也能处理（见习题1.7）。

②电压原的引出端，如同电压表的引出端一样，假定由同种材料制成。引出端由不同材料制成的情况也不难处理，只要把V_电源定义为用理想电压表接在电源两端所测得的电压即可。这样，式（1.4.11）和式（1.4.12）仍然成立（见习题1.8）

首先我们考虑图1.15α的外加偏压为零的情况。自由电子的浓度在n侧高，在p侧低。因此它们企图扩散穿过两侧之间的边界（在图中为向下运动），同时在n侧留下带正电的不可动的电离施主，如图所示。同样地，空穴企图从其数量很充裕的p侧向上扩散到n侧，同时在p侧留下带负电的不可动的电离受主。为简单起见，常常假设这种现象导致在一个边缘分明的区域里载流子完全耗尽，如图所示。这种情况称为耗尽近似，而这一区域称为耗尽区。在n侧电离施主越多，它们的总电量越多，因而它们产生的电场越强，它们施加在企图向下扩散的电子上的吸引力也越强。同样地，在p侧的电离受主越多，它们对企图向上扩散的空穴的吸引力也越强。这种过程的最终结果是：在两侧都有足够的杂质原子呈离化态，因此它们所产生的强电场阻挡了载流子进一步的净流动。于是，耗尽区的宽度就固定下来了，并且外部导线中的电流为零。值得注意的是，如果切断外部导线，这种结构的内部情况也不会改变。事实上，在这种情况下，根据式（1.4.6）以及有关的讨论，不难看出，在此结构中的三个接触电势互相抵消了，在两个开路的端子之间不存在静电势差。

当没有外加偏压时 耗尽区两端（从n侧深处到p区深处）的电势差将仅仅是n型材料对p型材料的接触电势，这个电势称为结的内建电势^②，用Φo来表示。根据表1.1和式（1.4.4），Φo用下式给出

式中ΦFP和ΦFn分别为p侧和n侧的费米势。我们将对两侧中有一侧是重掺杂区的情况感兴趣。我们提醒读者，在这种“简并”半导体情况下，式（1.4.2）或式（1.4.3）都不能应用，请看这些公式后面的说明。在实践中，可以选择Φo以使得那些包含Φo的表达式与实验结果达到最佳的一致。

令在结两侧的耗尽区的深度为ι1和ι2，如图所示。如果结的截面积（从顶端往下看）为A，在n侧的耗尽区部分的体积等于（ι1A），而施主离子的总数等于（ι1A）ND。由于每个这样的离子带电荷+q，所以那里的总电荷，用Q1表示，为

类似地，在耗尽区的p侧的总电荷（由受主离子所带）为

因为总体上为中性，所以必然有

现在我们注意力集中于n+p类型的“单边突变结”，也就是ND》NA的突变结。ND》NA这一关系与式（1.5.2）至式（1.5.4）等合在一起指出

这意味着，实际上全部耗尽区都伸展进入了p侧。

现在可以对耗尽区应用泊松方程（1.2.13），假设这里的所有电荷都是杂质离子所引起的（附录C）。我们发现，在这里考虑的ND》NA情况下，结两端的电势差Φo实际上全部降落在p侧。若用Φ2表示降落在p侧的电势差，则我们有

①在每一方向上电流导通的良好程度不能从接触电势的数值推断出来。有关金属-半导体接触处的导电性的理论是相当复杂的，并且是一个有争论的主题^［5.16］。

②确切地说，应该称为内建电势差。

还可看出，长度ι2范围内的受主原子必定呈离子态，以维持式给出（附录C和习题1.13）：

式中∈s由式（1.2.14）给出。

现在我们定义p侧单位面积的电荷Q′2如下①：

根据式（1.5.3），（1.5.7）和（1.5.8）可得

式中

利用式（1.2.10）和（（1.2.14），可算得硅的F值为0.00579fC.μm^-1/2.V^-1/2。

其次来考虑如图1.15b所示的施加正向偏置电压V>0的情况。现在平衡被打破了，这一极性的偏置电压势必产生一个与杂质离字所形成的电场相反的电场。假设欧姆接触的接触电势差不受影响，则耗尽区两端的静电势差将从中Φo减小至Φo-V，因此沿回路静电势之和保持为零。于是，在每一点上，总电场减小，载流子更容易扩散穿过边界。n侧的电子（在介侧电子是多数载流子，因而，可大量提供）向下扩散；p侧的空穴（在p侧空穴是多数载流子，因而也可大量提供）向上扩散。这两者运动的结果是产生一个向上的正电流，如图所示。要使这一点有意义，当然应该回想起前而所作的关于所有可动的载流子已经全部离开耗尽区的假设仅仅是一种方便的简化而已；实际上，在“耗尽区”中，还有可动载流子存在，且能维持电流的流动。假设电流不太大，以及耗尽区外的半导体中的欧姆电势降落被忽略，则可证明，此电流值将由下式给出^{［2-10，12］}

式中Io是取决于结构细节的一个电流量，且随温度的升高而增大，Φt是热电压，由式（1.2.8）给出。

图1.15b中电源的极性是为了对n侧提供附加的电子，这些电子将去还原某些原先已电离了的施主原子，因此包含施主离子的区域变窄了。根据电中性原理，在另一侧的一部分受主离子也将被空穴还原。因此耗尽区的宽度较图1.15α中的小。这一点与我们前面所说的在每一点上电场强度降低是一致的。

现在再来考虑图1.15c所示的情况，这里从n侧端到p侧端加上一个反向偏置VR>0，这结构也是处于不平衡的。现在所加电压的极性是为了与图1.15α。相比增加每点上的电场强度，这一极性势必会使电子向上移动离开耗尽区的上边缘，同时使空穴向下移动离开下边缘因此耗尽区的宽度将增加，如图所示。VR越大，耗尽区变得越宽。如果n区为重排杂区，整体上的电中性表明，宽度的增加主要发生在p侧。根据这一点也可说明p侧耗尽区承受了大部分电压降。

①这里导出的结论以后将被扩展ι2随水平位置而变的情况中去。在那种情况下。我们必须用微商来定义每一水平位置上的Q2'为dQ2/dA（原文dQ2'/dA有错，译者注）

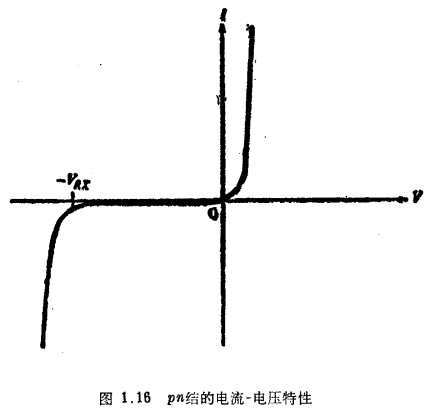
可以看出，现在的电场方向是使电场不再帮助多数载流子像在正向偏置时那样，从每一侧向着结的边界流动。相反，在n侧靠近耗尽区边缘的少量空穴（少数载流子）被电场往下扫。类似地，在p侧，靠近耗尽区边缘的少量电子被往上扫。来自每一侧的少数载流子的流动产生了一个方向与图1.15b相反的净外部电流，由于少数载流子供应很少，所以这一电流很小。式（1.5.11）对于反向偏置仍适用，只要使V=-VR就可以了。当VR大于几倍Φt指数项可忽略，电流看起来“饱和”了，其值为-Io。由于这个原因，Io常常称为饱和电流，实际上，各种“非理想因素”使得实际的反向电流值大于Io，甚至有点取决于VR值。反间电流强烈地依赖于温度，温度每增加10℃或甚至更少些，Io就加倍。如果VR超过某一值VRX，用于推导式（1.5.11）的理论^［4-9，12]就失效了。此时pn结中产生一个从n侧流向p侧的大电流，称为“反向击穿”。VRX称为反向击穿电压，对于MOS集成电路中遇到的结，它的典型值为10~100V，与制造工艺有关。图1.16是包括击穿在内的pn结的完整的I-V特性曲线。在MOS集成电路中，大多数pn结的反向偏置电压VR<VRX，它们的反向电流可以忽略，除非应用于极端临界状态或者温度很高。然而要注意，图1.15c中的反向电流是非平衡状态的一种表现形式，不管这一电流如何小，它总是在结和外部电池之间提供了联系，这种联系剧烈地改变了零偏压下平衡状态时原有的条件。因此，在平衡状态时适用的关系式，诸如式（1.2.6）或者式（1.2.7），总的说来不再适用于非零偏压下的情况。

在反向偏压VR下，耗尽区两端的静电势差（图1.15c中的ψc）将增加VR，因此沿回路所有电势降落相加仍为零（在欧姆接触处的接触电势差认为不变）。因此有

新的耗尽区宽度可由式（1.5.7）给出，不过式中的Φo要用新的ψc来代替（附录C），即

p侧新的耗尽区单位面积电荷，同样地可由下式而不是用式（1.5.9）来给出：

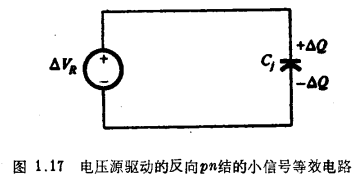
下面我们来考虑反向编置pn结的小信号电容的概念。如果反向偏压增加了一个小的增量ΔVR，则耗尽区的宽度必定在两侧都有所增加，为增加宽度所需移动的电荷必定会流过外部电路。更准确地说，n侧另有一部分施主原子将成为离子，从而增加了n侧的总电量。为了实现这一点，外部电路必定要把电子从靠近耗尽区的顶部边缘移走，因此有一负电荷，比如说-ΔQ从结的顶端离开。这一现象可以等效地说成有一相反的正电荷+ΔQ从结的顶端流入。同样地，由于反向偏压增加，在p侧额外一部分受主原子必定变为离子。为了实现这一点，外部电路必定要把带正电的空穴从靠近耗尽区的底部边缘移走，这意味着有一正电荷+ΔQ流出底端，或者等效地说，有一负电荷-ΔQ流进底端。因此，图1.15c中电荷Q1和Q2的变化量为：

现在假定在如图1.17所示的电容器两端连接有一个电压源，其电压等于反向偏压的变化量ΔVR，电容器的电容值选得使它的两极板上的电量为+ΔQ和-ΔQ，即分别等于当反向偏压由VR变为VR+ΔVR时通过顶端和底端进入pn结的电荷。于是，这一电容就代表了反向偏置pn结的小信号电容。如果用Cj表示这一电容，则有

运用式（1.5.16），且把有限差值变为微分，重新定义Cj，则有

最后，用截面积A除以等式两边，便得单位面积的小信号电客Cj/A，并以C′j表示：

现在把式（1.5.12）和（1.5.14）代入上式，得

利用式（1.5.12）和（1.5.13），上式也可写成另一种形式：

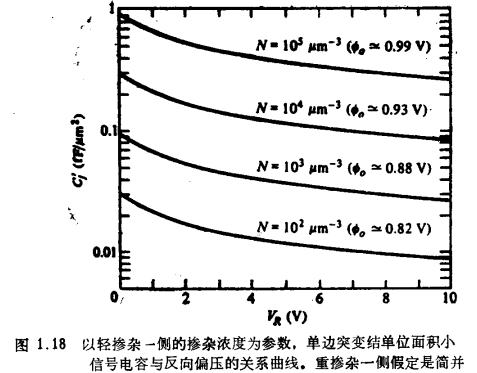
C′j和VR的关系绘于图1.18，图中Φo的近似值是给定的^［5］，假定重掺杂一侧是简并的。如果C′jo表示C′j在VR=0时的值，则式（1.5.20α）不难转换为如下形式：

再强调一次，上述结果是对单边突变结导得的。对于从n侧到p侧渐变的更复杂的掺杂情况，可以证明C′j近似为：

式中C′jo的表达式将取决于n侧到p侧掺杂变化的细节（这些细节形成了所谓结的掺杂剖面）。αj的值对于我们已讨论的单边突变结为1/2，对于线性缓变结（在结中，净杂质浓度随垂直位置线性地变化，在两侧的边界处为零）是1/3。对于实际的掺杂分布（既非恰好是突变，也非恰好是线性缓变，）常常如此选择参数αj，C′jo及Φo，即使得式（1.5.22）与实际测量能吻合得最好。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助