接触电器几种材料串联中的作用及其结构

接触电器几种材料串联

现在我们可以来进行一项有意义的观察，即考虑几种材料的串联，如图1.14α所示，如前所述，所有材料都处于同一温度。如果我们把电势差ψ_KL用这串联结构中的各接触电势来表示，则有

然后在上式中重复运用式（1.4.4），可得：

显然，在和式中，除ΦJ1和ΦJn以外，每个ΦJi都出现两次，一次为加，一次为减，因此有

① 在能得处现方法中，接施电势常用两种材料的“功函数”来表示。功函数WJ是表征材料J将性的一个量，它与把一个电学从该材样移动到真空中所需的能量有关，按照这样处理方法，图1.9α如中的ΦJ1，ΦJ2应或是（WJ2-WJ1）/q,其中q为电子电神量（附录A）。功高数很难精确测量，实际上，我们把它用于MOS精件建模时，不得不对它“修正”，我们把选用“真空”（它与我们将要研究的高件关系甚少）为参考材料改为用更恰当的材料（本征桂）为参考材料，从面避免了讨论的复杂性。如果读者喜欢用功的数，毫无疑问，只要把ΦJ定义为-WJ/q，式（1.4.）中的差值奶然是正确的。

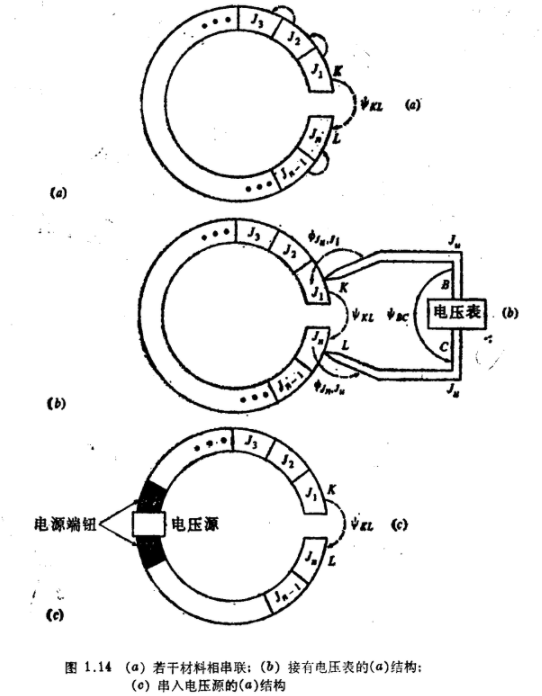
这里产生一个问题，即我们能否用一只普通的电压表来测量电势ψKL？答案是不可以，即使这电压表假定是理想的（也就是说，该表不从测量电路中取用任何电流）也不行，这一点可从图1.14b中看出。假设该表的引出头用某种材料Ju制成，则这两个引出头之间的电势差ψ_BC（这是该电压表所“看见”的电势差）是

把式（1.4.4）代入上式，有

再把式（1.4.7）代入式（1.4.9），我们得到

总之，不论回路中有多少种材料，其两端的静电势差只决定于第一种和最后一种材料，而且不能用普通的电压表来测量^①。对于这类测量，必须采用特殊的技术^［14］。

现在要问，如果在回路中插入一个电压源，则ψ_KL等于多少？这一情况表示在图1.4c中，这电源的引出端假设由同种材料制成。用沿回路绕行的方法可得

此式应与式（1.4.7）相比较^②。

如果一只像图1.14b那样的理想电压表接在图1.14c中的K和L两点上，则该表将测得什么？此时，式（1.4.9）仍然适用，其中的ψ_KL上用式（1.4.11）给出，于是我们有

此式应与式（1.4.10）相比较。

现在可以清楚地看到，当我们分析电路时，为什么只要所有接触点都处于同一温度下，接触电势就似乎从未画进电路图中。像在推导式（1.4.12）的例子中所见的那样，这种电势抵消了，不能用普通的电压表测出，也不能计入电路方程。但是，在研究电子器件的物理过程时，必须计及接触电势，除非发生偶然的抵消现象，否则忽略接触电势会导致误差。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助