电子技术论坛
信息来源: 时间:2022-5-25
半导体扩散工艺基础技术原理概述分析
漂移仅仅是半导体中形成电流的两种机制之一。另一种机制是扩散,它发生在当粒子的空间分布不均匀时,即存在“浓度梯度”时,粒子的随机运动促使它们从浓度高处向浓度低处扩散。注意,这种现象不是由电场引起的,因此与粒子是否带电无关。例如烟雾粒子就显示出这种扩散现象。然而,如果这些粒子带了电,如电子和空穴,则扩散引起了电荷的运动,因而产生了电流。
让我们借助于图1.8α来考虑扩散的起因。假设一块具有宽为b厚为c的矩形横截面的半导体中存在电子,这些电子在任意垂直平面(如图示一平面)中是均匀分布的,但沿半导体的长度方向分布不均匀。现假定不存在空穴,并且这块半导体只在左、右两端与外界发生联系,以便使其中的电子分布保持固定不变,这一分布可用一固定的n与x的关系图来表示。在未作进一步说明以前,我们假设这一图形为如图1.8b所示的直线。
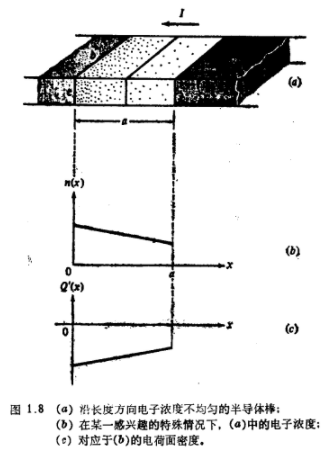
在图示平面的两边都有电子,且在随机地作热运动,但是在紧靠这平面的左边,长度Δχ很小的平行六面体内所包含的电子多于紧靠平面右边同样的平面六面体内的电子。因此可以预期,在给定的时间间隔内,从左向右穿过平面的电子要比从右向左多,这一过程对应于电子自左向右的净流量。由于每个电子带一个负电荷,因此定义为图中所示方向的电流是正的。这一电流正比于每个电子所带的电荷量q和载面积b,而且n随χ变化的斜率越负,正的电流值越大,事实上,I正比于(-dn/dχ)。这样,我们有[1-11]

式中D为比例常数,称为扩散常数。这一常数与迁移率μB之间可用所谓爱因斯坦关系式联系起来[1-11]:

式中Фt是热电势,由式(1.2.8)给出。对于空穴扩散,有类似的关系式;当然,对应于各自迁移率的空穴扩散常数和电子扩散常数在数值上是不同的。注意,如果图1.8α中所示的粒子是空穴,且它们的浓度向右递减,则将有从左向右的空穴运动。由于空穴带正电,因此这一运动将相应产生一个与图示方向相反的电流。
如果n与x不是直线关系,那么dn/dx,因而扩散电流还将随位置而变。于是,扩散电流必须写为I(x),但仍等于式(1.3.1)的右边部分。稳态时,由于在任意x点处的总电流必须相同,因此在这种情况下,必然存在一个漂移电流分量,此分量随位置而变化,以致使总电流(扩散电流和漂移电流叠加而成)与x无关。一般情况下,半导体中的电流是漂移和扩散两者共同作用的结果(例如,两种机制都可以在一个pn结中遇到);不过,往往其中一种机制是主要的。为简单起见,在本节其余部分,我们假定只存在扩散电流,因此n与x的关系为一直线。
下面我们考虑图1.8α中x点处的体积为bcΔx的一垂直薄片材料,此薄片中的电荷为(-q)n(x)bcΔx,这里负号对应于负的电子电荷。把这薄片电荷除以薄片的顶视面积bΔx,并使Δx趋于零,便可得到单位面积电荷,它是x的函数:

它与x的关系见图1.80c。把式(1.3.19)和式(1.3.18)代入式(1.3.17)可得

现在来考虑更一般的情况,即允许电子浓度在垂直方向上分布不均匀。假设在任意给定深度处的一个水平面上,n与x的关系仍为直线(我们假定图1.8中在垂直于纸面的方向上,n仍是均匀的)。由于现在n沿垂直方向是不均匀的,因而电子在垂直方向上有扩散的趋势,但是,我们将假定有一个合适的外加电场来阻止电子的这种扩散。换句话说,我们假定电子仍只平行于x方向运动,因此层流得以保持下去。这样就不难证明式(1.3.20)仍然适用①。
由于Q′(x)与x的关系为一直线,它的斜率为

把此式代入(1.3.20),得

因为在式(1.3.20)后面已经说明,当假设n是x和垂直位置两者的函数时,式(1.3.20)仍然成立。同样,式(1.3.22)也应该成立。
渡越时间了现在就不难计算了。不难证明,在任意时刻,半导体棒内的总电荷为

于是根据式(1.3.2),渡越时间为

本书中,我们常对在x=α处电子浓度减至零的“彻底下降”情况感兴趣,即

①我们考虑这材料由水平平行薄片组成,在每一海片内部,n沿垂方向是不变的。如果ΔI和ΔQ′(x)表示这种薄片上单位面积的电流和电荷,则我们有 。总电流I将是各个ΔI之和,并可把总和式中的ΔQ′(x)合在一起以给出材料在x处的总的单位面积电荷Q′(x)。更精确的做法是把ΔI和ΔQ′(x)变为微分,并进行积分,这样我们便可得到式(1.3.20)
。总电流I将是各个ΔI之和,并可把总和式中的ΔQ′(x)合在一起以给出材料在x处的总的单位面积电荷Q′(x)。更精确的做法是把ΔI和ΔQ′(x)变为微分,并进行积分,这样我们便可得到式(1.3.20)

对于这一特殊情况,式(1.3.24)变为

注意,这一形式与式(1.3.10)十分相似。
联系方式:邹先生
联系电话:0755-83888366-8022
手机:18123972950
QQ:2880195519
联系地址:深圳市福田区车公庙天安数码城天吉大厦CD座5C1
请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号
请“关注”官方微信公众号:提供 MOS管 技术帮助




