运算电路乘法器算术及其应用电路解析

在数字信号处理中经常会遇到数据与系数相乘的运算，如傅立叶变换、卷积等。如果用普通计算机软件来实现，就必须按程序进行多次的加法运算，速度很慢，不能满足实时高速讯号处理的要求。

硬件乘法器可以大大提高运算速度，已成为数字信号处理（DSP）和高速计算机中的重要部件。

一、算法

乘法器由两部分电路组成：其一产生多项部分积；其二把这些部分积合成最终积。有多种算法产生不同的部分积形式，部分积的数目应尽量减少，以提高产生最终积的效率。最终积是用一个加法器阵列进行计算而得，阵列的结构也与算法有关。

我们以为例，说明有关乘法器的算法。其中x为被乘数，Y是乘数，均为N位的二进制数。

最简单的算法是取Y中的一位yi，由低位到高位，yi与X相“与”，产生N项部分积，与一般多位乘法相同，yi每增加一位，部分积左移一位，把这些部分积加起来得到2N位最终积。这种算法的加法阵列比较大，运算次数较多，速度较慢。

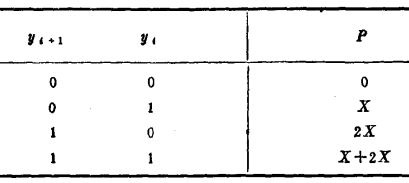
为了缩小加法器阵列，必须减少部分积的数目，其方法是每次在乘数中多取几项与X相“与”产生部分积。以取两项（yi，yi+1）为例，部分积项可以减少一倍，但当yi，yi+1=1时会产生两项部分积X和2X。具体结果如下页表。

由此可见，当乘数“1”成串时部分积的项数不能减少。

改进波茨算法就是为解决上述问题而提出来的。“1”成串的乘数可以进行如下的交换：

k位长的“1”字串可以简化成两项，一加一减。利用这种变换，可在所取乘数的低位（或高位）加上一位考察位。例如，_yi+1=yi=1作为某一次部分积的乘数，考察位_yi-1=0，由此得变换式：

yi+1、yi这两位产生的部分积就是-X，y_i+2的进位在下次求部分积时被补偿。下次取乘数y_i+3和y_i+2，y_i+1是考察位，如果y_i+1，则表示上次用了变换进位，这次变换时y_i+2上必然会加1，由此自动补偿了上次在y_i+2上的进位。

这样从低位到高位每次取两位，附加考察位，进行重叠扫描，在最低位要补上y_-1=0作为首次取乘数y₁、y₀时的考察位。每次总共考察三位，相互重叠一位。

考察三位，八种组合的改进波茨算法的编码表如下，由它们可以得到相应的部分积Pi：

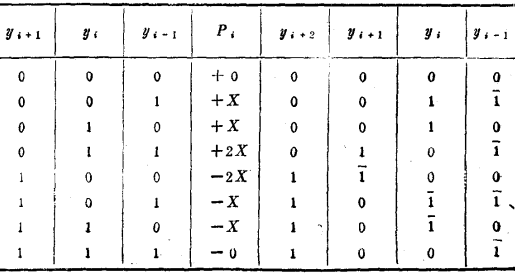
用上述方法可以减少一半部分积，但亦需要付出代价，在0、X以外还要加上+2X、-2X和-X三种部分积，因此需要按上表进行译码，这种译码电路叫波茨译码器。对负项要采用补码运算。由于乘数取两位，所以每次得到的部分积较上次结果要左移两位，最后进行总加。

当然每次取乘数可以不止两位，这样部分积的项数还可以减少，但部分积的种数也会增加，使波茨译码器变得十分复杂，结果并没有好处，所以目前普遍采用取两位乘数的改进波茨算法。

当y_i+1=1时得负项，减法化为加法，即求反加1，故可变为求反加y_i+1。当y_i+1=0时，得正项，在加法运算时y_i+1项对运算完全没有影响。若以8位乘8位为例，其部分积的产生方法是先将其LSB和MSB各扩充一位y-1和y8，它们均为零。然后按图4.21将乘数分成互相重叠的五组，前四组均有三位，最后一组只需要两位。由此产生的五项部分积为A、B、C、D、F，由它们组成改进波茨算法的各部分积项的加法格式如下：

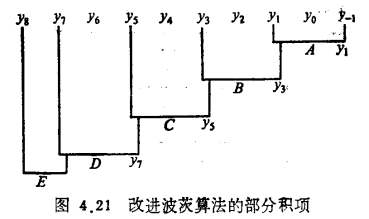
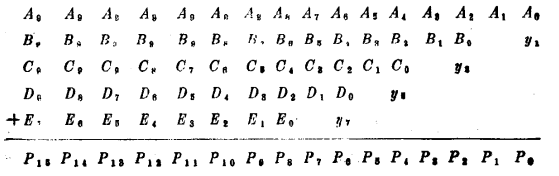
部分积有±2X，因此其字长为9位，即A0至A8，第10位A9为符号位。在做减法补码运算时，其符号位应扩充至最高位（第16位），再加上相应的y_i+5，即y₁。B、C、D、E也按此规律产生。8×8的最终积为16位，即P15P14…P0。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助