电子技术论坛
信息来源: 时间:2022-3-3
MOS管器件弱反型次开启特性及关系式分析
早期就有人发现,在长沟MOS器件中IDS随VGS不是突变的,而是有一段缓冲过渡区,如图1.36所示。此过渡区就是弱反型次开启区。它在原理上是不难理解的,因为早先模型中,人为地定义 作为开启条件,这是强反型条件。当
作为开启条件,这是强反型条件。当
 时表面就开始反型,将
时表面就开始反型,将 称为弱反型区,并有弱反型电流。
称为弱反型区,并有弱反型电流。

下面将对弱反型电流进行定量分析。图1.37为弱反型条件下的表面能带图。 为沟道电位。
为沟道电位。
存在 条件下的弱反型区:
条件下的弱反型区:
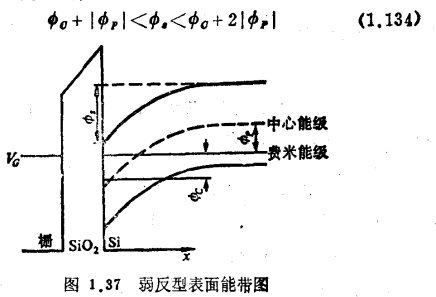
表面区的泊松方程为:
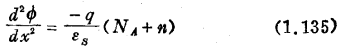
为了简化计算,近似地假设在 强反型条件下,表面电子浓度为
强反型条件下,表面电子浓度为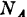 ,即有分布函数
,即有分布函数

(1.136)代入(1.135)
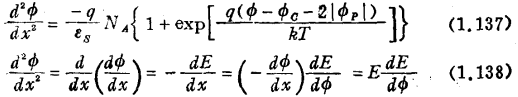
(1.138)代入(1.137),积分

上式后面一项的指数项可略去,由此得:

 为表面的面电荷密度,其中有可动电荷Qm及不可勒的耗尽电荷QB,因此有
为表面的面电荷密度,其中有可动电荷Qm及不可勒的耗尽电荷QB,因此有

对弱反型, ,因此可对(1.140)中的指数项进行台劳展开:
,因此可对(1.140)中的指数项进行台劳展开:

上式中的 与
与 相关联。为了求解Qm,必须将上式中的
相关联。为了求解Qm,必须将上式中的 用
用 表达出来。
表达出来。

略去 项,将
项,将 在
在 附近展开:
附近展开:

令 ,其中Cd为耗尽层电容,它是工作点的函数。
,其中Cd为耗尽层电容,它是工作点的函数。

令

则有:

将(1.146)代入(1.141),得弱反型的 与
与 的关系式
的关系式

当 时进入强反型区,这时有:
时进入强反型区,这时有:

上式对 展开后:
展开后:

由上式得强反型的可动电荷 表达式:
表达式:

其中 也是随
也是随 加大而加大。
加大而加大。
为了达到 和
和 连续,可求出两者过渡点的
连续,可求出两者过渡点的 ,可证明该点的
,可证明该点的 为
为

令 为强反型的起点,将它和(1.150)一起代入(1.147):
为强反型的起点,将它和(1.150)一起代入(1.147):

令 ,代入上式则有:
,代入上式则有:

其中 为一个系数,应有
为一个系数,应有
在SPICE中为了达到电流在 处连续,将系数采用类似强反型的电流公式,只是将原来公式中的
处连续,将系数采用类似强反型的电流公式,只是将原来公式中的 换成
换成 得弱反型
得弱反型 :
:

严格求 应该对
应该对 进行积分计算,这里不给推导过程,只给出结果:
进行积分计算,这里不给推导过程,只给出结果:

从上式可见,弱反型电流 随
随 呈指数增加,因而具有很大的跨导
呈指数增加,因而具有很大的跨导 电流随着
电流随着 增加也逐步趋向饱和。
增加也逐步趋向饱和。
(1.154)可化成更常用的简化公式:

其中

图1.38是 特性。由图可见,当
特性。由图可见,当 ,(室温为78mV)时
,(室温为78mV)时 就达到饱和,因此工作在次开启区的电路可以在低压下工作,这对一些微功率电路是十分有利的。电路的功率可表示为交流和直流两部分之和:
就达到饱和,因此工作在次开启区的电路可以在低压下工作,这对一些微功率电路是十分有利的。电路的功率可表示为交流和直流两部分之和:

对CMOS电路来说,Io直流漏电流很小,可略去,因此功率P随工作电压VDS下降面平方关系降低。
联系方式:邹先生
联系电话:0755-83888366-8022
手机:18123972950
QQ:2880195519
联系地址:深圳市福田区车公庙天安数码城天吉大厦CD座5C1
请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号
请“关注”官方微信公众号:提供 MOS管 技术帮助




