电子技术论坛
信息来源: 时间:2022-3-2
MOS管电路模拟中电荷模型的组成基础
电流与电荷之间的关系为:

在进行数值计算时设下标为端点,上标为牛顿迭代次数。采用梯形近似式:

进行线姓化,得电流迭代式:

将(1.116)式代入上式,得

并定义

为端点l与m之间的电容k次迭代值。但是,这个电容Clm已失去本身的意义,只是作为展开系数。
(1.118)式可简化为:

其中

(1.120)式代入结点的导纳矩阵可求解 ,其中应注意电容系数的不可逆性,即
,其中应注意电容系数的不可逆性,即
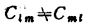
这也是与真正电容的重要不同特性之一。
由电荷守恒律得:

利用(1.115)式可得:

利用(1.123)式可得如下关系式:

为了说明上式的来源,我们以l=G为例变化时,由(1.123)和(1.124)式得:

由此可得到:

由于存在(1.126)关系式,因此12个电容系数中只有9个是独立的。
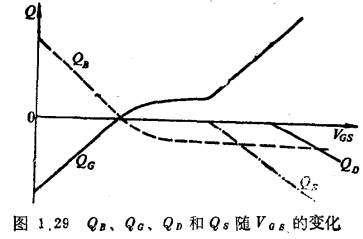
根据前面 在各工作区的表达式,图1.29画出。QD、Qs、QG和QB在不同VGS工作区的变化曲线,图1.30为CGB, CGD及的变化曲线。
在各工作区的表达式,图1.29画出。QD、Qs、QG和QB在不同VGS工作区的变化曲线,图1.30为CGB, CGD及的变化曲线。
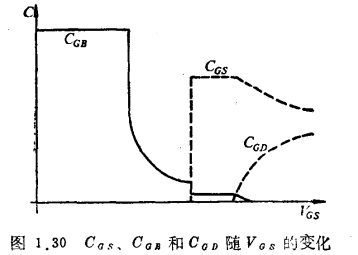
为了看到电容的不可逆性,图1.31对CGD与CDG进行了比 较。从图可看出CGD和CDG不相等。在饱和区  ,这是因为沟道已夹断,VD当然不会影响QG。然而,CDG >0,因为VG改变必然引起 ld的改变,从而改变用QD。用(1.110)式对VGS微分得饱和区的
,这是因为沟道已夹断,VD当然不会影响QG。然而,CDG >0,因为VG改变必然引起 ld的改变,从而改变用QD。用(1.110)式对VGS微分得饱和区的 。
。



