电子技术论坛
MOS管沟道电荷QC的分割公式分析详解
信息来源： 时间：2022-3-1
MOS管沟道电荷QC的分割公式分析详解
MOS管沟道电荷QＣ的分割
QC可以积分求得，如(1.88)和(1.91)式，而要把科学地分割成Qs和QD就比较复杂。
为此，采用瞬态分析法。在S端和D端分别有：
其中
为t时刻仅与r时刻的端电压有关的稳态值。
为了求解Qs、QD，列出沟道各点的电流方程：
如不考虑复合损失,则有：
积分上式：
将（1.98）式代入上式：
从0到L积分上式：
改写上式中的积分：
上式代入（1.100）式，并令其中的y=L,则有
对比(1.102)、(1.103)和(1,96)、(1.97)式,可得
将
的表达式代入，并将dy转换成
，即
,进行积分计算。由此可得MOS管在各工作区的Qs、QD分割后的公式：
1、线性区
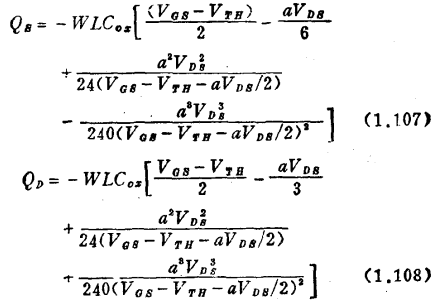
2、饱和区
由以上三式得：
在SPICE程序的MOS本征电容模型中取系数
的原因就在于此。
以上推导中实际上作了准静态近似(QSA)。它假设低频下电荷分布北(对)的瞬态响应用稳态解来近似，即端电压变化时沟道电荷分布随即跟着变化。显然，准静态近似对高领工作情况不适用，因为电荷再分布跟不上端电压的变化。
计算证明，在高频下。QS、QD的分割与密勒模型的结果基本一致：
1、饱和区
2、线性区
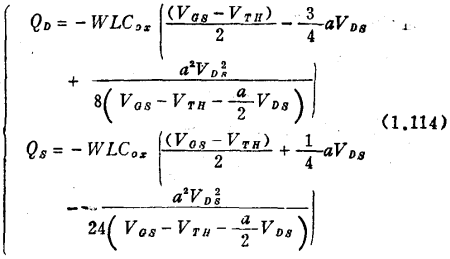
对短沟器件来说，它的电荷再分布速度快，倾向于采用QSA近似。例如，当L=1μm时，在10GHz以下可用QSA近似。但是,对于长沟器件必须根据工作频率选用Qs、QD的公式。