MOS管沟长调制效应饱和的长沟-短沟采取不同近似方法

当时，从漏端开始沟道被夹断或速度达饱和 （对短沟器件），有效沟道长度随之减小。VDS越大，越小。正是由于随VDS（大于）的增加而减小，引起输出饱和区特性曲线上翘现象。如图1.19所示，这也是饱和区具有有限输出阻抗的主要原因。

由IDS公式可知，，因此沟长调制效应可表示为：

其中ΔL就是在条件下引起的有效沟长的缩短量， 是起始饱和点的。

由（1.67）式可知，同样ΔL的情况下，L越短，沟长调制效应越严重，输出阻抗越低。

ΔL的计算比较复杂，也要解二维或三维的泊松方程。因此， 要用严格的数值求解法对电路模拟是不现实的，一般采用在某种近似模型下再加拟合系数的办法。

根据不同的饱和机理，对长沟、短沟采取不同的近似方法。

1、夹断饱和（长沟器件）该模型计算ΔL的方法如图1.26所示。要求算出在漏区（VD）到夹断饱和点之间的电场强度ET。这是一个载流子耗尽区，应有

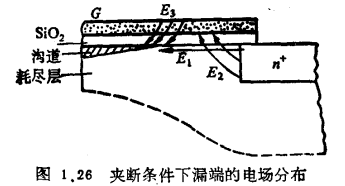
如图1.26所示，ET由以下三部分组成：

（1）漏区反偏pn结耗尽电场E1；

（2）漏到栅边缘场在水平方向的分量E2；

（3）栅到夹断点边缘场在水平方向的分量E3。于是有

也上述说明可得:

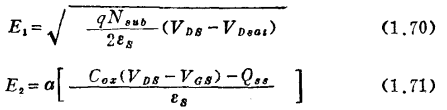
其中a是边缘场系数，约为0.2；

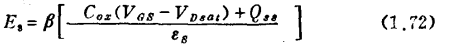
其中β也是边缘场系数，约为0.6。

由此求得ET及ΔL，再由（1.67）求出IDS及输出阻抗。

2、速度饱和（短沟器件）首先假定从漏区到饱和点之间可动电荷基本上被耗尽掉，图1.27示出这种饱和的模型图。在此基础上再进一步近似为一维问题，然后解一维泊松方程：

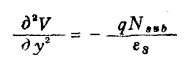
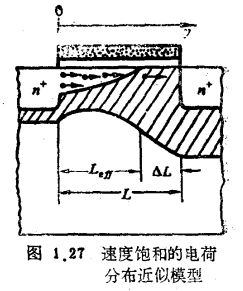
其边界条件为：

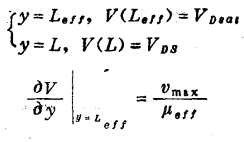
求解上述边界条件下的泊松方程，可得：

其中。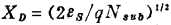

要注意(1.73)式中的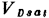不是常数，而是VDS的函数，即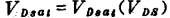。这是因为随着增加，则缩短，由此使达到的电压，即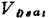也会随之减小。这样使求成为解复杂的非线性方程问题。因为先要求出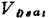,应该用(1.51) 式。但在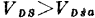情况下，(1.51)式中的L将改为,因此从(1.51)求 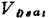又需要知道。这样，必须在(1.73)和 (1.51)之间多次迭代求解。SPICE的MOS 2模型中规定了采用两次迭代求解法，以节省机时。先令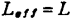,利用(1.51)式 求出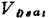，再由(1.73)式求出，以此利用(1.51)重新求出新的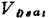，再由此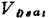用(1. 73)求出。

由于在计算中作了过分的近似和简化，即使用上述方法求出及输出阻抗，与实测的结果仍旧相差甚大。为此，必须引进拟合系数使与实测结果基本相符。

在SPICE中引入系数修正及：

其中为大于1的系数。它的引入使ΔL适当缩小。这是合理的，因为在解一维泊松方程时略去了边缘场的影响，使计算的ΔL比实际偏大。的确定方法是使计算的输出阻抗与实测基本相符，达到拟合的目的。

实际上，短沟器件的输出阻抗或饱和特性上翘不仅决定于沟长调制效应，而且还与前述的DIBL效应密切相关。这是因为VDS成增加使开启电压VTB下降，由此也造成IDS的增加。

由于影响短沟器件的饱和特性的因素比较复杂，很难推出具有相当精度的计算公式，所以在电路模拟中常采用一些半经验简化公式：

其中为起始饱和电流，λ是一个拟合系数，实际上是 饱和区的微分导纳。λ为越大，输出阻抗越低。显然λ为与沟长L密切相关，L越小，λ越大。

式（1.75)过于简单，而且λ本身与L又有函数关系，使用起来也不太便利。为此有人提出了精度较好的改进公式如下：

其中

，为衬底杂质浓度；

，均为实验决定的经验常数。它们可以根据工艺条件作适当的调整。

公式(1.76)比(1.75)的优点在于它的系数和都是与L无关的量，可以适用同-VLSI中各种L的饱和特性的描述。