MOS管饱和区特性及处理短沟器件的有三种方法

当VDS增加到足够大时，IDS由线性区进入饱和区。众所周知，大尺寸器件因漏区被夹断达到饱和，β和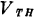与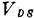无关、进入饱和区的标志为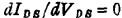，由对（1.43）式微分而得饱和电压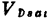和饱和电流的表达式：

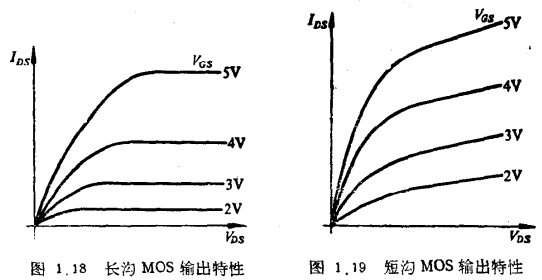
实验表明，短沟器件的饱和特性与大尺寸器件有很大的不同，这是因为两者饱和机理不同所致。图1.18和图1.19分别画出它们的输出特性的实测结果。由它们的对比可见，短沟管有如下主要三点不同之处：

1、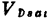与不呈平方关系，而近似呈线性关系。

2、饱和电压和饱和电流均小于大尺寸公式（1.45）和（1.46）的预期值。

3、饱和区IDS不平坦，而有明显上翘趋势。沟道越短。上翘越快，即输出阻抗越低。

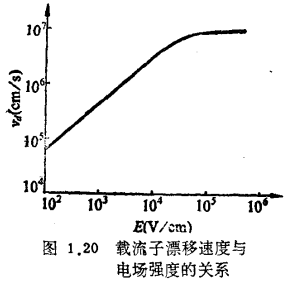
产生上述差别的主要原因在于两者的饱和机理不同。长沟器件是夹断饱和，而短沟器件是载流子漂移速度饱和。这是因为在夹断前短沟器件内的电场强度很大，载流子漂移速度因散射几率增大而达到饱和。图1.20为载流子漂移速度与电场E的关系。

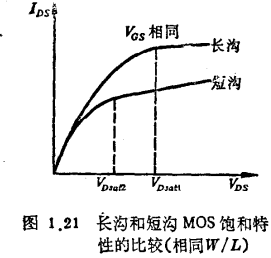
由于在短沟情况下载流在速度饱和先于沟道夹断发生，因此和均较长沟公式的计算值低。图1.21画出了两种饱和特性的比较。在短沟情况下，迁移率和均与有关，因此不能象长沟器件那样简单地导出它的和表达式。

有三种方法处理短沟器件的饱和特性：

1、迁移率突变模型

这是在SPICE中MOS2所用的近似模型。它近似假设载流子迁移率在达到饱和速度以前保持常数，而达到后则微分迁移率突变为零。图1.22就是此模型的载流子漂移速度与的关系，并与实际的曲线进行比较。显然这是一个为计算方便而建立的简化模型。如图1.22所示，实际上迁移率随电场是渐变的。

当时，漏端达到速度饱和，这是从线性区到饱和区的临界转变状态。在已知漏端载流子速度的条件下，可求得：

其中为沟道中速度达饱和点的可动面电荷密度。在临界状态时饱和点在漏端。

根据（1.3）式得的表达式：

代入（1.47）式：

在临界点上也可用线性区的IDS公式（1.38），可得：

在临界点应有，则有

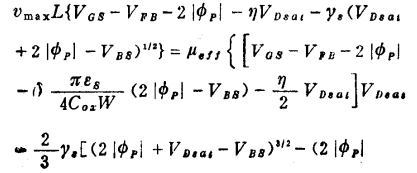
在已知（约为5×10⁶cm/s）的条件下，利用上式可以求解，再由（1.49）或（1.50）求解。

当时，速度饱和点向源端方向移动，这时从源到饱和点之间的距离为有效沟道长度，引起增大，这是沟长调制效应所致，本章第六节将作专门的分析和讨论。

2、迁移率渐变模型

上面MOS 2所用的迁移率突变模型与实际的物理过程差别较大，因此带来较大的误差，特别在临界转变点附近更为突出。

图1.23为用突变模型计算和实际的输出特性的比较。由图可见，突变模型近似使转变点附近变化比实际快得多，使线性区部分电流偏大。因此，有必要采用一个较为精确的渐变模型。

该模型将载流子漂移速度与沟道中横向电场E的关系分成两段：

其中是达到饱和值的临界电场。图1.24画出表示上述关系的曲线，它与实际的曲线比较接近。

可用表示为：

将式（1.53）代入（1.52），可得：

因为，故上式可化为

上式两边积分可求得

当达到时，漏端电场为将及代入（1.54）式，可得：

当时，（1.55）式的。由此可以从（1.55）和（1.56）联立求解：

其中

由（1.57）式代入（1.56）可求出。从（1.57）式可见，随L和的减小而降低，这与实验的结果相一致。同时从（1.56）看到与不呈平方关系，而近似呈线性关系。

3、半经验公式处理

把速度饱和效应体现在和的公式（1.45）和（1.46）的系数a中，令

其中μ₁为表征速度饱和效应的系数，它与横向的电场强度有关。

即为原来公式（1.44）中的a。

当沟道内横向电场很强，速度饱和起主要作用时，，则

代入（1.46）可得：

由此得到与之间的线性关系。由于在速度饱和时必有正比于，所以系数是一个与成反比的量，并由实验提取。

以上三种处理速度饱和方法确有优劣之分：突变模型误差大，公式复杂；渐变模型物理概念明确，但公式亦比较复杂，半经验方法公式简单，与实验一致性较好，较普遍被采用。

顺便说一下，SPICE MOS3中的渐变模型，它用作为E/Ec，从物理意义上来说是很不确切的。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助