MOS场效应半导体表面的空间电荷与电场强度解析

应用-维泊松方程的解，可以计算在外加垂直电场作用下半导体表面附近的空间电荷区、可动载流子浓度和电场强度之间的关系¹。MOS表面的空间电荷。对于结构如图2.1所示的简单MOS电容器，假设x=0规定为硅-二氧化硅的界面，同时假设外加栅极电压的所有变化都足够缓慢，使整个系统总是处于热平衡状态，此时硅中的静电势 ф 与单位体积内总空间电荷密度ρ之间的关系可用泊松方程：

表示。式中∈_s是硅衬底的介电常数。电场强度和静电势之间的关系是：

半导体内总空间电荷密度是深度x的函数，可以写成单位体积离化施主浓度ND⁺与单位体积空穴浓度p之和，再减去单位体积离化受主浓度NA^-与单位体积电子浓度n之和，然后整个乘以电子电荷q。

在硅衬底体内深部，静电势和电场强度都近似等于零，必然存在电荷中性条件。因此对于非常大的x值，有下式成立

假如费密（Fermi）能量和费密（Fermi）能级都用常规的方式，即从禁带能隙中心来确定。此外，对于硅体内深部非常大的x值，自由载流子密度由

和

给出，式中 ф_F 为费密电势，n_i为硅本征载流子浓度，为玻尔兹曼常数，T为开尔文（Kelvin）温标温度。

如前所述，对于非常大的x值，静电势近似等于零。在x=0时的静电势记为ф_s，x=0时，量ф_s=ф通常称为表面电势。MOS表面的空间电荷。例如，如考虑图2.2所示的p型硅衬底的情况，ф_s将随正栅极电压的增加而增加，并且ф_s可以看成是因外加栅极电压的作用而在硅表面上发生的能带弯曲程度的直接量度。

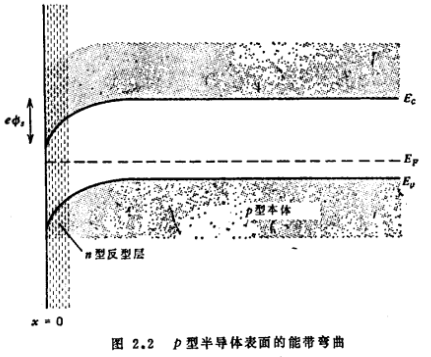
假设衬底中的所有杂质都已离化，这对处在室温或高于室温下的硅是正确的，那末结合（2.4）和（2.5），考虑ND⁺=ND^-和NA^-=NA，得到

^·此处不考虑电子有效质量和空穴有效质量以及能带底状态数和能带顶状态数的差别——译者注

在硅表面附近，静电势 ф 的不再为零，单位体积电子和空穴浓度分别等于

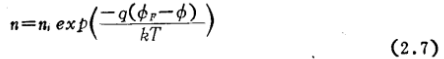
和

因此，在硅内静电势取任意值时，单位体积电子和空穴浓度之差等于

应用（2.1），（2.3），（2.6）和（2.8），泊松方程即可写成

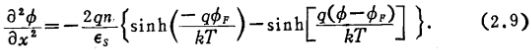
为了简化起见，我们规定：

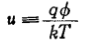
因为，所以（2.9）变成

本征德拜长度定义为

对于硅而言，本征载流子浓度和本征德拜长度与温度的函数关系，分别如图2.3，图2.4所示。

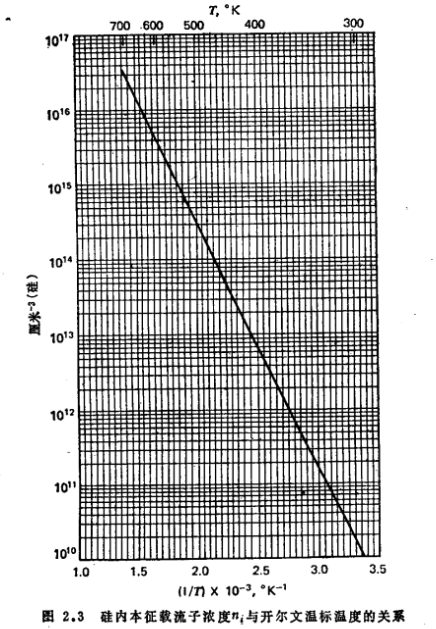
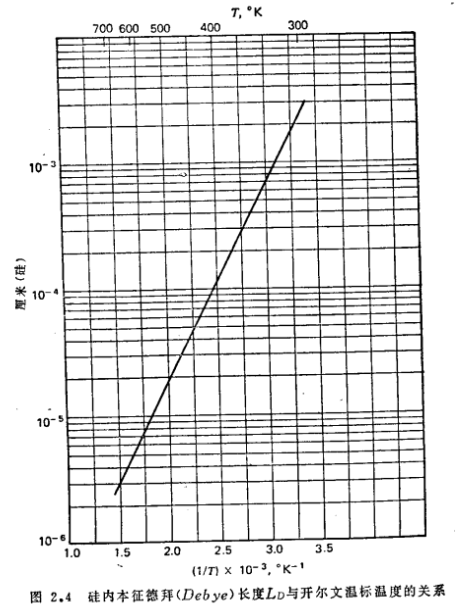
应用上述本征德拜长度的定义，泊松方程可以改写成

由硅衬底体内深处积分到表面得到

或

从（2.2），硅中沿x方向的电场强度等于

因此（2.15）式开方后取负根得到

在硅表面x=0，u=us电场强度等于

应用高斯定律，硅中用来终止这个电场所需要的单位面积的总电荷密度是

是表面反型层单位面积所包含的电荷密度，QSD是表面耗尽层单位面积所包含的电荷密度。应用（2.12），（2.17），和（2.18）得到p型硅衬底中单位面积的总表面空间电荷密度的表示式

表面空间电荷密度对p型衬底为负，对n型衬底为正。

·“密度”两字估计系 原文遗漏——译者注

如调节外加栅极-衬底电压，使硅表面还未形成反型层，硅表面实际上处于本征状态（即，фs=ф_F），则，而表面耗尽区电荷密度变为

对于足够大以致可以形成表面反型的栅极电压，（n型）反型层电荷密度可以写成²：

式中x定义为在硅衬底中ф=ф_F，而使硅处于本征态的点。注意us=u（x=0）和u_F=u（x=x）。从（2.7）和（2.10），量n（u）du可以表示成

将代入（2.16）得到

因此结合（2.21），（2.22），和（2.23）可以得到反型层（n型）单位面积电荷密度。这个结果是

对于n型衬底，p型表面反型层单位面积（正）电荷密度Qp，也可以得到类似的表示式。表面空间电荷区的总电荷密度等于反型层电荷密度与耗尽区电荷之和

式中由（2.19）给出，Qn由（2.24）给出。格罗夫（Grove），迪尔（Deal），斯诺（Snow），和萨氏（Sah）已经证明，对于较高的表面势，与相关的所有电荷密度实际上都集中在反型层内2。

亦即

物理意义是，在平衡条件下反型层一经形成，任何由于提高外加栅极电压而增加的表面电荷将集中在反型层内，从而导致表面电导的提高。MOS表面的空间电荷。因此，在表面发生反型之后，耗尽区电荷密度QSD趋于饱和，达到一个常数，同时表面耗尽区宽度也趋向常数（极大）值。

假设表面耗尽区单位面积电荷密度在发生强反型之后（ф≌2ф_F空20p）达到最大值Qs0。时而趋向饱和，同时假设在达到上述饱和情况以前，表面空间电荷区内的所有电荷皆集中于耗尽区，因此用ф≌2ф_F代入（2.19）得到

在典型条件下，并且，因此

应用（2.12）和（2.27）给出

因为

在强反型发生后表面耗尽区最大宽度与QSDmax之间的关系是

因此，表面耗尽区最大宽度等于

总括地说，对于采用p型衬底制作的并在平衡条件下工作的MOS结构，假如外加栅极电压仅使产生表面耗尽区，那末耗尽区单位面积电荷密度等于

此式也可表示为

式中xd为表面耗尽区宽度

对于可使表面电势大于或等于2ф_F的栅极电压，并且硅表面出现强反型，。因此

此处QSDmax由（2.29）近似地给出，Qn由（2.24）近似地给出。以上对p型衬底所使用的步骤，完全适用于n型材料制作的MOS结构，并推导出QSD，xd，Qp，QSD_max和xd_max类似的表达式。

如导带与价带有效质量差别忽略不计，硅衬底中费密电势的绝对值近似等于

式中N为衬底单位体积的有效杂质浓度（N=|ND-NA），具有p型或n型硅衬底的MOS结构的与N的关系如图2.5和2.6所示。

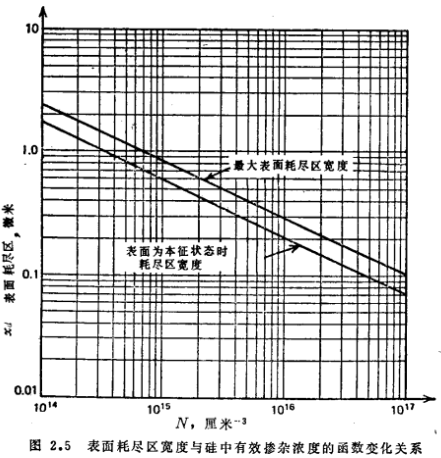
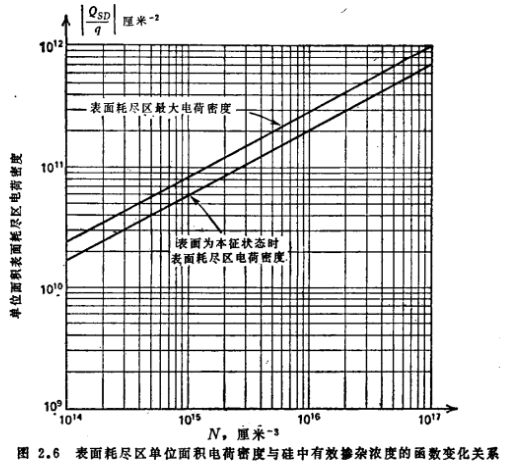
联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助