MOS场效应晶体管带通放大器电路的设计及原理

为了简单起见，以一级单调谐放大电路为例，并用最常见的y参数表示法来说明带通放大器（调谐放大器）的设计基础——稳定性、增益和频率特性。

（1）放大器的稳定性

图2.24是在输入部份和输出部份都使用单调谐回路的单级放大器的原理图。在这里下述公式成立。

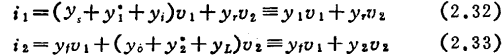
式中y1、y2为单调谐回路的导纳（略去角注）可写作

^●）给出Gma的Г s、Г L

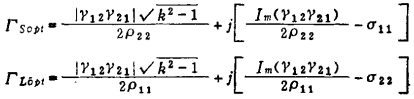
此值在参数置换中不是不变量。Gma的另一种表达式为式（2.55）。

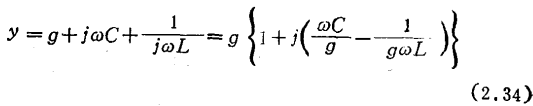
代入调谐角频率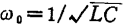和回路的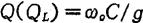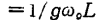，则y可表示为

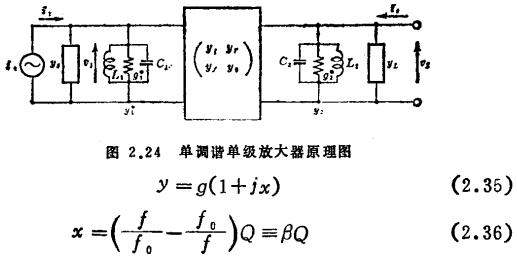
x为规一化的失谐率^●），一般等于。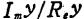

在图2.24，为使放大系统稳定，整个网络的输入导纳yin的实部应取正值。若设i2=0，yin可由下式给出。

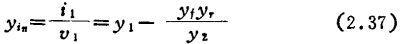
设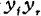的相角为θ，稳定条件可表示为

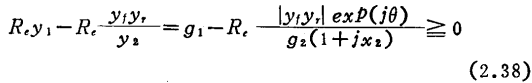
当频率在fo附近变化，从而x也变化时，从第二项的矢量轨迹可知^●●），

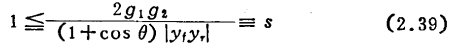
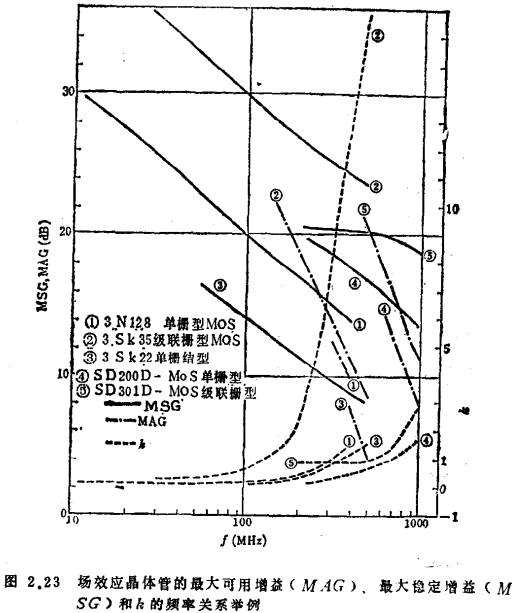
S称为斯忒恩的稳定系数。条件（2.39）与式（2.21）所示的K大于1具有同一内容。s表示振荡所需要的反馈电压与实际反馈电压之比，在参数置换中不是不变量。MOS管带通放大器的设计。放大器输入端和输出端的调谐频率不同，各自的Q值也不同，另外在复调谐等情况下，具有较式（2.39）更宽的稳定范围，所以用式（2.39）进行判断较为稳妥。在实际放大器中，为防止器件和电路参数的偏差而引起的不稳定性或者由于频率特性的关系（参阅本页），s以大于4为宜。

^●）在fo附近狭窄的频带内，β可近似为

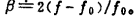
^●●）利用输出导纳的实部为正的条件，也可得到同样的结果。

y_T不为0时的输入导纳，可用式（2.37）表示，所以当输出电路的调谐频率x2=0时，有

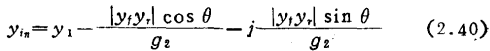
为了消去出现在输入端的虚部，要增加值为j ▏y_fy_T▕ sinθ/g2的电纳部份。也就是说，必须进行调谐补偿^●）。以后以这种经调谐补偿的放大器为讨论对象。

（2）转换增益

如用前节的符号以y参数改写转换增益表达式（2.27），则有

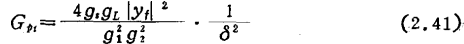
式中

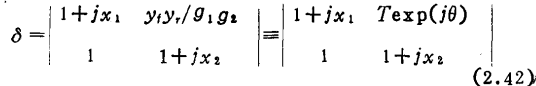
δ为表示频率特性的项^●●）。

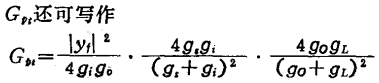
^●）与输入端调谐时的输出端补偿相同。

^●●）假定在所考虑的频帮内y参数不变。

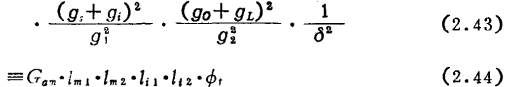
式中Gam为忽略y_T时的最大可用增益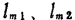，为失配损耗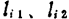，为调谐回路的插入损耗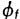^●），为反馈的影响。

在中心频率fo，

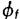为

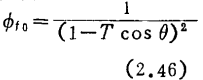
1/δ频率特性，当T改变时的计算举例示于图2.25。MOS管带通放大器的设计。图中也标出S值，随着T增大、S变小，与中心频率产生偏离，失去对称性。在此意义上1/S值有时也称为偏离因数。

（3）最大可用增益

在保证器件绝对稳定时，为得到Gma，对信号源导纳和负载导纳。

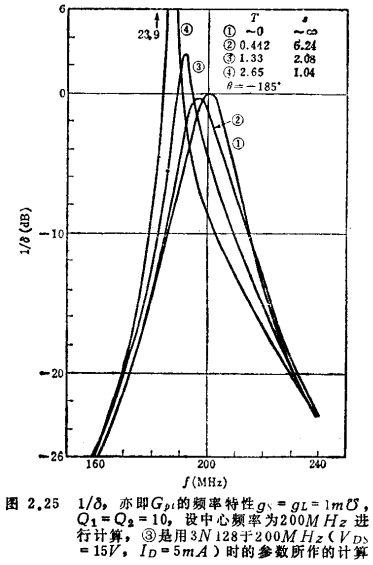
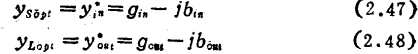
在输入输出共扼匹配的条件下进行计算。此时

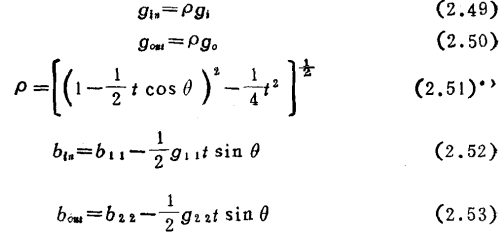
式中

Gma还可用下式表达（假定匹配电路无损耗）

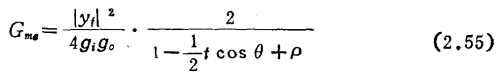
（4）使放大器稳定的方法^●●）

当器件有潜在不稳定性时，为使其稳定，有用中和减弱反馈的方法以及使输入输出失配的方法。

最常用的有y参数中和法。y_T处于第3象限时，将输出的相位反相，经中和元件Y反馈到输入端（参照图2.26（a））。

若设Y值为

（n为输出线圈的匝数比），则包括中和电路的y参数为

●）此式有意义的情况是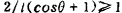：，即器件处于绝对稳定的状态。

●●）此处再次忽略匹配电路的损耗。

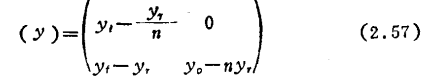
而

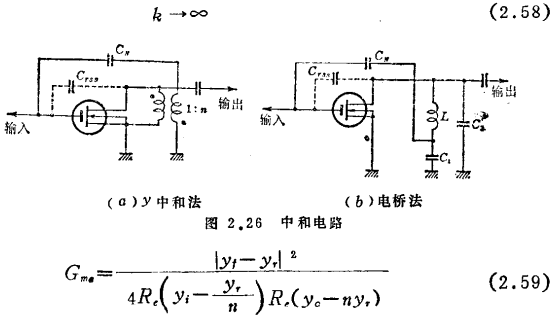
Gma最大时的n值为

另外，在图2.26（b）所示的电桥电路中为中和条件。

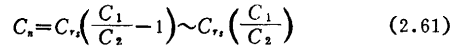
用失配方法实现稳定的一例有雷歇（Rathi）的方法^12）。取S为恒定值来设计最大的。根据结果，当输入输出的失配为同一量级时，可获得最大的1+m值为

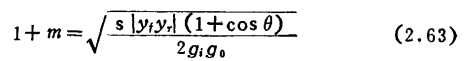
此时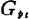，可写作

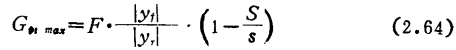
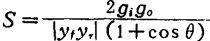（器件固有的稳定系数）（2.65）

式中

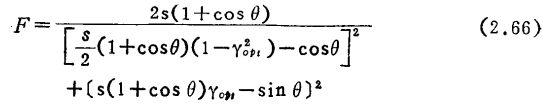
而

是由方程

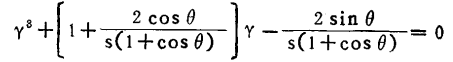
给出的实根最佳值。文献（12）中有用图表示的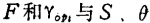的函数关系。

（5）多级放大器

由n级构成的多级放大器的转换增益为第一级的转换增益与以后各级功率增益之积。

功率增益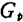由调谐时的式（2.26）给出

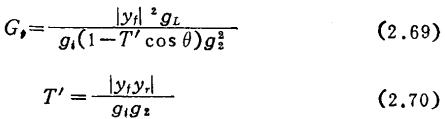
在第一级中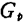，值与输入电路的转换功率增益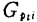（调谐时）

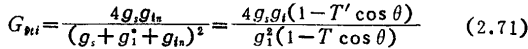
相乘，则有

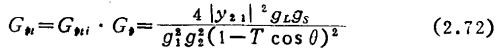
与由式（2.41）所得结果相等。

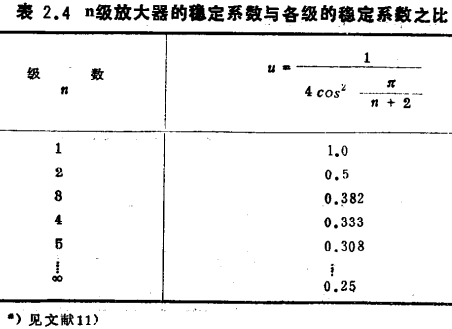
关于稳定性的问题，以回路增益为核心进行分析时^●），为得到稳定的放大，应选取适当的稳定系数量级。MOS管带通放大器的设计。多级稳定系数为一级稳定系数除以表2.4所示的值u。

（6）单调谐选择回路的频率特性

图2.27所示的单调谐选择耦合电路，以下述两式为设计的基准。

传输效率：

调谐回路的插入损耗：

式中

QL为有负载的Q，Q=ωL（gs+gc+gL）（2.75）

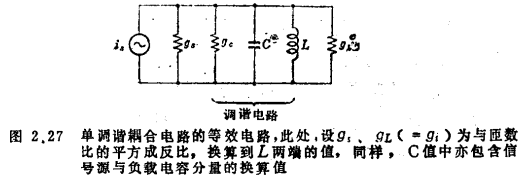
Qu为无负载的Q，Q=ωLgc            （2.76）

失配损耗：

m：失配比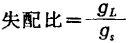

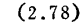
相位变化：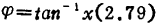

-3dB带宽B可由式（2.73）求得为

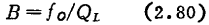
用放大部件接成n级放大器时，总的一3dB带宽B。与各级的B的关系为

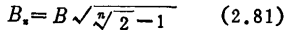
各级的QL为（参阅图2.28）

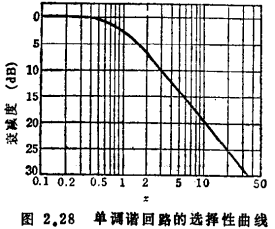
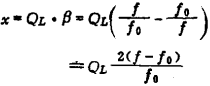
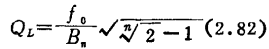
^●）此处设gs、gL为与线圈距数比的平方成反比，换算到C两端的换算值。并设C值中包含信号源与负载的电容分量换算值。fo、x，即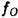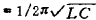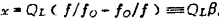，。另外，在考虑调谐回路的选择性即放大系统的选择性时假定反馈没有影响。

（7）复调谐回路的特性

复调谐回路与单调谐型相比，可得到在频带内平坦而在频带外陡峭下降的特性。它的基本形式是图2.29所示的M耦合型和C耦合型两种。

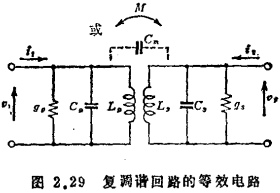
设图中的gp、Cp、gs、Cs为与此回路相连的器件的输入输出导纳在Lp、Ls两端的换算值。耦合系数k的定义为

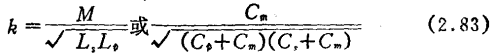
如选谐振频率ωo为

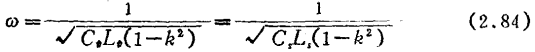
（对于M耦合，用Cp+Cm、Cs+Cm置换Cp、Cs），此网络的y参数为

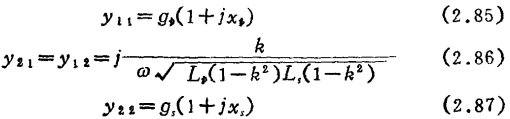
式中

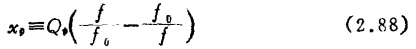
由此而得的输入、输出导纳为

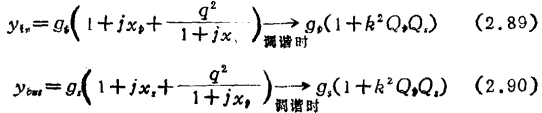
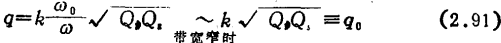
转换阻抗Zo为

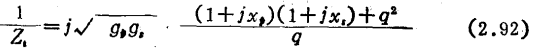
如计算1/Zo的振幅特性，当

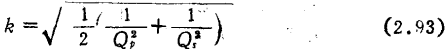
时，则呈现最大平坦特性（临界耦合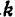），比此值小时为单峰特性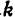，比它大时为双峰特性。

特别是当Qp=Qs=Q时，

给出振幅平坦特性，另时给出延迟平坦特性。

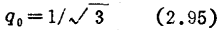
图2.30示出Qp=Qs时的幅度特性。

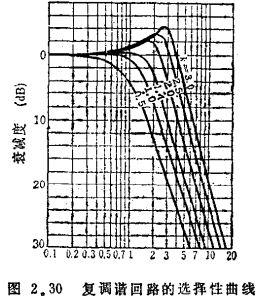
这种耦合回路的传输效率，可通过转换功率增益的计算，由下式求得

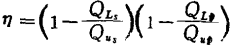
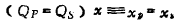
（8）“L”形电抗邦合电路

如图2.31所示，用纯电抗元件接成“L”形的匹配电路，由于结构简单，适于作试验用电路或在固定频率下使用。将任意频率的导纳变换成其它任意导纳的这类网络在两种以上。可根据频率特性的要求，选择其中任意一种。

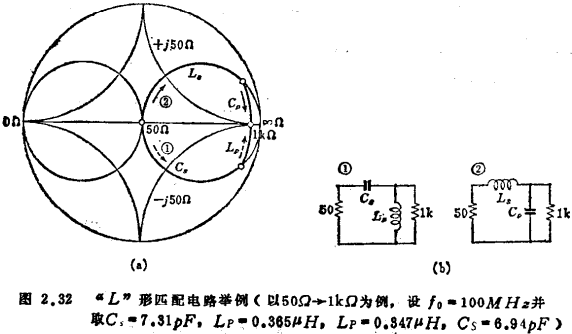
“L”形耦合电路用图2.32（a）所示的表示阻抗和导纳的史密斯圆图进行设计，极为方便。如图2.32所示将50Ω的特征阻抗变换成1kΩ的电路有①②两种、这两种电路在中心频率附近的特性是类似的，但偏离此频率就大不一样，①变为高通型，②变为低通型，可根据要求来选择。MOS管带通放大器的设计。同样的耦合方式很多（例如借助c分割的阻抗变换法等），细节请参阅其它书籍。

以上对一些基础知识进行了叙述，以下按不同目的所用的不同设计方法进行叙述。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助