电荷传输现象的数值解式及分析详解

今考虑MOS二极管I下面积累着衬底的少数载流子——空穴，在与之相邻的MOS二极管Ⅱ上加一传输电荷用的脉冲，使空穴由MOS二极管I向Ⅱ传输的情形。由于在MOS二极管I上加上了供电荷传输用的脉冲，MOS二极管I下面的反型层内几乎不产生指向MOS二极管Ⅱ的电场，而是可等效地说，MOS二极管I下面积累空穴的势阱壁在与MOS二极管Ⅱ邻接的部分相应地降低了。所以，空穴传输的原动力是起因于空穴间相互斥力的场和空穴在空间分布的不均匀而产生的扩散。

设反型层内载流子集中在界面，呈δ函数分布，如对其余的空间电荷层作耗尽层近似，则硅与二氧化硅界面电势ψs与外电压VA之间有如下关系式:

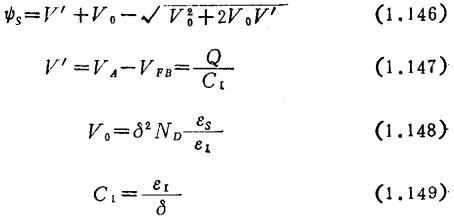
式中

VFB为MOS二极管的平带电压

Q为存在于界面处的载流子的面电荷密度

δ为二氧化硅膜厚度

ND为硅衬底的杂质浓度

ξ1为二氧化硅的介电常数

ξs为硅的介电常数

而电流方程为

式中，χ为由MOS二极管I指向II的座标

可将这些公式联立求解。

为使问题尽量简化，首先对式（1.146）进行线性化

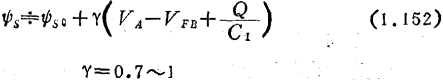
上式确实是相当好的近似。沿硅表面的电场Eχ除微分式（1.152）所得之值外，尚有载流子相互间斥力所产生的部分。如果也考虑到金属栅电极所产生的镜象力，则载流子之间相互排斥产生的电场ER（χ）可表示为

结果

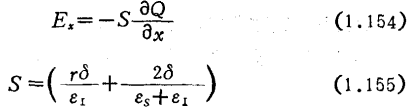
如设MOS二极管I两端为x=0和x=L，简单的边界条件有

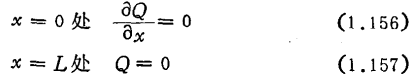
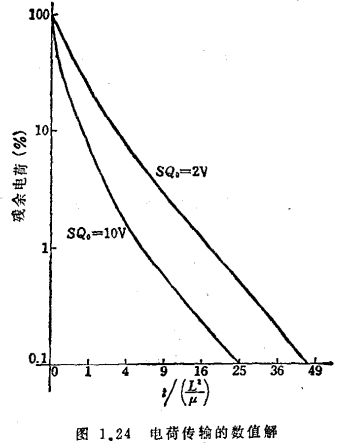
在这种边界条件下的数值计算举例如图1.24^15）。在传输初期，SQ0=2V时与SQ0=10V时的传输速度相差5倍，这意味着传输开始时电荷传输是靠空间电荷引起的斥力使载流子漂移的，而在传输终了时传输速度由扩散所左右。

这样的过程也可半定量地进行分析。将式（1.154）、（1.155）代入式（1.156），得

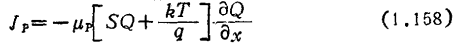
考虑到传输开始时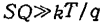，，上式可简化为

同时假定Q的分布是线性的

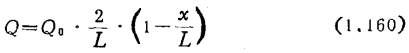
式中Qo为各时刻积累在MOS二极管I的空穴总量，于是有

另一方面，将式（1.150）从x=0到x=L进行积分，并注意到Jp（0）=0，则得

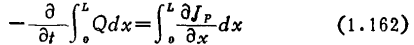
即

若用式（1.161）求Jp（L），结果为0，所以要以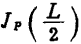值推测Jp（L）值，于是有

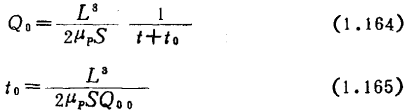
Q00为Q0的起始值

由以上可知，起始电荷越多。电荷的传输就越快。

在传输的终期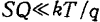时，式（1.158）变为

此式系纯粹的扩散方程，其解为

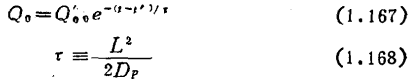
Q00是t=t'时Q0的值，t’是传输速度原理上变为由扩散控制的时刻。为方便起见，确定t’时，取式（1.164）给出的Q0与式（1.167）给出的Q0无突变连结的时刻。

目前，电荷耦合器件正在飞速发展中。正在从各个方面对电荷耦合器件进行研究，诸如从改善其使用方法方面，如减少相数，提高传输效率以及加偏置电荷等方面进行研究。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助