电子技术论坛
信息来源: 时间:2021-3-26
MOSFET沟道内载流子迁移率与栅电压的关系
至此,对于沟道内载流子迁移率μch并未过多涉及,而将它视作常数。但沟道内载流子迁移率的值比对大块硅晶体测量的值μB要小,且测得随栅电压和漏电压而变化。μch与栅电压的关系以及μch较晶体体内值为小这两点是紧密联系着的。因此,要对这一问题进行讨论。
已经知道,不仅半导体表面反型层内载流子的迁移率,而且于薄膜所观测到的迁移率也比大块晶体测得的迁移率要小。可以认为两者共同的原因是表面散射。但是,这种表面散射如系图1.10(a)所示的镜面反射(specular reflection);由于沿表面方向的载流子动量不发生变化,从而沿表面方向的导电现象不因表面的存在而改变,因此载流子迁移率也不因表面的存在而变化。另外,如图1.10(b)所示,假如不发生沿表面方向有动量变化的散射,载流子迁移率不因表面的存在而发生变化。
图1.10(b)所示的反射之所以在表面各处产生,必然是表面的凹凸不平作无规分布。表面的粗糙度和空间分布的波长,与入射载流子的波长相比若充分地小,入射载流子是不受这种粗糙度的影响的。因而发生的是镜面反射。沟道内载流子迁移率。若与入射载流子的波长相比是足够长时,从宏观上看就不能说是均匀的表面了,就要考虑与入射电子的波长大致同一量级的粗糙度。对硅表面反型层而言,入射电子的波长为数十埃量级,可以认为有这一量级的表面粗糙度存在。当存在载流子漫散射时可通过求解漫散射边界条件下的下述玻耳兹曼输运方程求出电流方程,再由电流方程算出载流子的迁移率
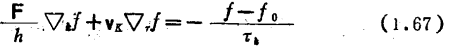
式中
F为加到载流子的力
h=h/2π,h为普朗克常数
⊿k ⊿r分别为k和r的微分算符。k为电子的波矢。r为电子的位置矢量
f 为电子的分布函数
fo为热平衡时电子的分布函数
vk为波矢为k的电子速度
τk为散射的弛豫时间
对硅表面反型层而言,如图1.11所示,取硅表面为z轴的原点,向硅体内方向取为z的正值,边界条件当z→∞时,虽f→fo,但在表示z=0处漫散射的表现方法上存在问题。沟道内载流子迁移率。常用的方法是假设载流子在入射前不管有何种动量,经漫散射后的动量分布与入射前完全无关。
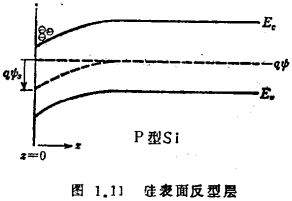
因此,假设经漫散射后的载流子的分布取与热平衡相同的分布,当

时,可认为

当电子的有效质量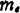 为标量,且τk与k无关,为一常数τ时,可对玻耳兹曼输运方程求解。今设沿表面方向的电场为
为标量,且τk与k无关,为一常数τ时,可对玻耳兹曼输运方程求解。今设沿表面方向的电场为![]() ,借此算出电流
,借此算出电流![]() ,则有
,则有
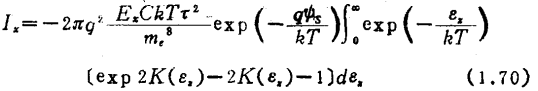
式中
q为载流子电荷
C为由![]() 定义的常数
定义的常数
ψ为静电势s为表面势
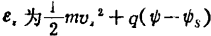
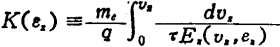 ,Ez为z方向的电场强度。
,Ez为z方向的电场强度。
为了使式(1.70)可解析地进行积分,Ez应为与z无关的常数Ezs,此时

式中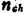 为表面反型层内的载流子面密度
为表面反型层内的载流子面密度
由式(1.71)可求出迁移率的解析式8),

如用图来表示可得图1.12中恒定电场,即三角形电势近似的曲线。由图可见,随着栅电压的增加,沟道中载流子的迁移率减小。但是Ez取恒定值的近似很不理想,如图1.12所示,它与假定抛物线形状电势分布经数值计算算得的结果有很大的差异,此点应予注意7)。

从物理学的角度看,对前述表面散射的理论存在着原则性的问题。也就是说,在MOS场效应晶体管通常的工作状态下硅表面形成反型层时,即便空间电荷层的厚度为微米量级,反型层的厚度也只有数十 到100
到100 的量级。另一方面,反型层内电子的波长也是同一量级,如图1.13所示,硅和二氧化硅间的势垒与硅中导带下端或价带上端之间可能形成电子的驻波。因而,反型层内的电子不能取连续的能量值,应取离散值。这种现象称为表面量子化。
的量级。另一方面,反型层内电子的波长也是同一量级,如图1.13所示,硅和二氧化硅间的势垒与硅中导带下端或价带上端之间可能形成电子的驻波。因而,反型层内的电子不能取连续的能量值,应取离散值。这种现象称为表面量子化。

这种量子化效应显著时,电子在垂直于半导体表面的z方向就不能运动,表面的电子只有沿半导体表面运动的自由度,电子处于二维状态。沟道内载流子迁移率。因此,不能想像电子与硅和二氧化硅膜界面的势垒碰撞后反弹回来的现象,所以前述的表面散射思路存在实质性的问题。
于是,如设 与栅电压的关系为
与栅电压的关系为

则有

因而

这是与式(1.15)相对应的关系式。
处于表面量子化状态的电子迁移率应取何种数值,有计及各种散射机制的理论,但还很难说这些理论对散射机制有透彻的理解。
联系方式:邹先生
联系电话:0755-83888366-8022
手机:18123972950
QQ:2880195519
联系地址:深圳市福田区车公庙天安数码城天吉大厦CD座5C1
请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号
请“关注”官方微信公众号:提供 MOS管 技术帮助