电子技术论坛
信息来源: 时间:2021-3-15
常见滤波器低通、高通、带通的设计方法及基本详解
RLC梯型网络的模拟法
1、低通滤波器
(1)三阶低通滤波器的设计
我们以三阶低通开关电容滤波器的设计为例,来说明低通开关电容滤波器的设计方法及步骤。三阶无源RLC梯型滤波器如图5.3-7a所示,它的节点电压和支路电流由下列方程式描述
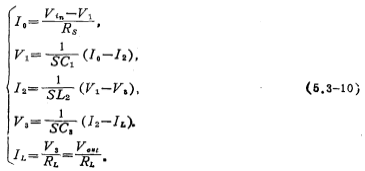
为使上式电流量变为电压量,引入比例电阻R,令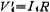 (i 为上式电流 I 的脚标)。这样上式写为
(i 为上式电流 I 的脚标)。这样上式写为
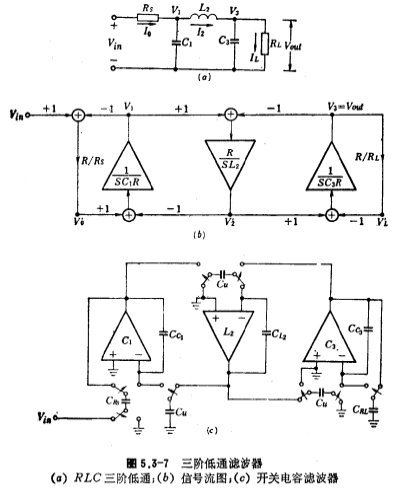
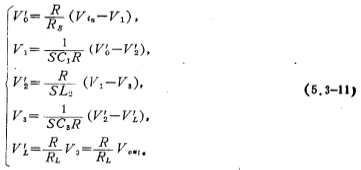
由(5.3-11)式可以得到如图5.3-7b所示的信号流图,图中有三个积分器,它们的时间常数分别为C1R、L2/R和C2R。对(5.3-11)式加以整理,可以得到如下方程式
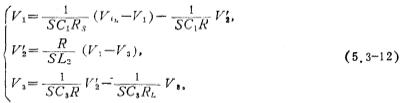
根据图5.3-7b所示的信号流图和(5.3-12)式以及RC积分器与开关电容积分器(图5.3-4)之间的转换关系,可以得到图5.3-7c所示的三阶低通开关电容滤波器。图中各级开关电容积分器就是图5.3-4所示的电路,为简单起见,将其开关画成另一种形式。低通、高通、带通。若该电路各级开关电容积分器的积分时间常数与(5.3-12)式中的积分时间常数相对应并使其相等,可以得到如下方程式:

对上式进行整理后得

式中fcx是归一化时(ωc=1弧度/秒)的时钟信号频率。在通常条件下,取Rs=RL=R=1欧姆,则(5.3-14)式写为

由(5.3-14)或(5.3-15)式可知,只要知道RLC梯型滤波器在归一化条件下的电感L、电容C、输入端电阻Rs和终端电阻RL,以及归一化后的时钟信号频率fcx,即可求得图5.3-7(c)电路中各开关电容积分器的电容比值。低通、高通、带通。为使开关电容滤波器特性与RLC滤波器特性接近,实际时钟信号f′cx应远大于低通滤波器的截止频率fc,其关系为

在归一化条件下,ωc=1弧度/秒,所以归一化后的时钟信号频率fcx有如下关系:

对于低通滤波器来说,一般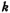 取20~40,如果
取20~40,如果 取得过大,则加大积分器的电容比,增加芯片面积。
取得过大,则加大积分器的电容比,增加芯片面积。
图5.3-7aRLC梯型滤波器参数可以在表5.3-1中找到。对于归一化(Rs=RL=1欧姆,ωc=1弧度/秒)三阶巴特沃思低通滤波器,具体参数是
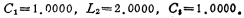
若取时钟信号频率f′cx与低通滤波器截止频率fc的比值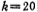 ,则由(5.3-17)和(5.3-15)式,可得到图5.3-7c中各开关电容积分器的电容比值,即
,则由(5.3-17)和(5.3-15)式,可得到图5.3-7c中各开关电容积分器的电容比值,即
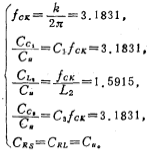
若取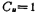 单位电容,则
单位电容,则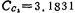 单位电容,
单位电容,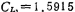 单位电容,
单位电容,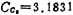 单位电容,
单位电容,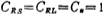 单位电容。
单位电容。
显然,单位电容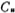 越小,则开关电容滤波器总的电容值也越小。但单位电容的大小受寄生电容大小的制约,不能取得太小,通常取
越小,则开关电容滤波器总的电容值也越小。但单位电容的大小受寄生电容大小的制约,不能取得太小,通常取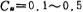 皮法。
皮法。
以上我们都是在归一化条件下进行计算的。若要对低通截止角频率ωc作频率变换,只要根据ωc值,并利用(5.3-16)式计算出实际的时钟颜率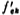 ,而对归一化求得的电容比值不器作任何修正。低通、高通、带通。其计算步骤是,首先在归一化条件下由(5.3-17)和(5.3-15)式计算出电容比,然后根据所需要的截止频率fc计算出实际所需的时钟频率f′cx。若上例的三阶低通滤波器的截止频率fc=1干赫,由(5.3-16)式可以得到实际时钟额率
,而对归一化求得的电容比值不器作任何修正。低通、高通、带通。其计算步骤是,首先在归一化条件下由(5.3-17)和(5.3-15)式计算出电容比,然后根据所需要的截止频率fc计算出实际所需的时钟频率f′cx。若上例的三阶低通滤波器的截止频率fc=1干赫,由(5.3-16)式可以得到实际时钟额率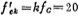 千赫。
千赫。
由上面讨论可知,对于开关电容滤波器来说,在确定了时钟频率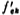 与滤波器截止频率fc
与滤波器截止频率fc
的比值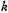 后,调节时钟频率
后,调节时钟频率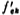 ,即可按
,即可按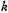 的比例系数改变滤波器的截止频率fc。
的比例系数改变滤波器的截止频率fc。
以上讨论了三阶低通开关电容滤波器的设计方法。无疑,采用类似的设计步骤,可以设计出高阶全极点低通开关电容滤波器。下面讨论椭圆函数低通滤波器的设计方法。
(2)椭圆函数低通开关电容滤波器的设计
椭圆函数低通开关电容滤波器是由无源RLC椭圆函数低通滤波器通过变换来实现的。
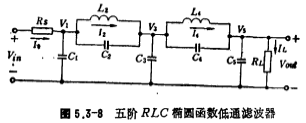
现以在通信系统中常用的五阶椭圆函数低通开关电容滤波器为例,说明其设计方法。图5.3-8是五阶RLC椭圆函数低通滤波器,其归一化元件值可由表5.3-3中找到。低通、高通、带通。由图5.3-8可以得到如下电压、电流方程式:
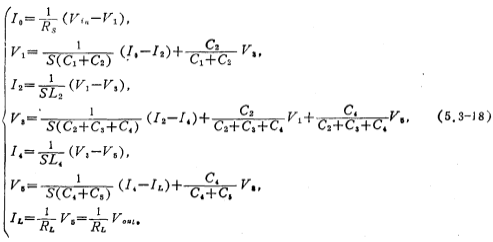
为使上式电流量变为电压量,引入比例电阻R,令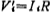 ,这样,(5.3-18)式可写为
,这样,(5.3-18)式可写为
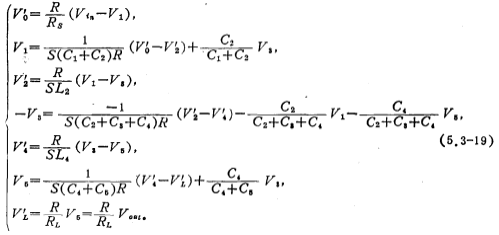
由上式可知,各电压之间的关系可通过积分器和加法器来实现。为便于选用有加法器的开关电容积分器,式中的V3改写成-V3。
根据(5.3-19)式画出的信号流图如图5.3-9a所示。图中积分器1、2、3、4和5的积分时间常数分别为(C1+C2)R、L2/R、(C2+C3+C4)R,L4/R和(C4+C5)R,各a值表示如下:
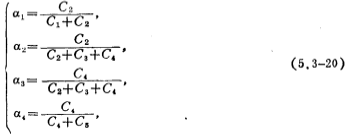
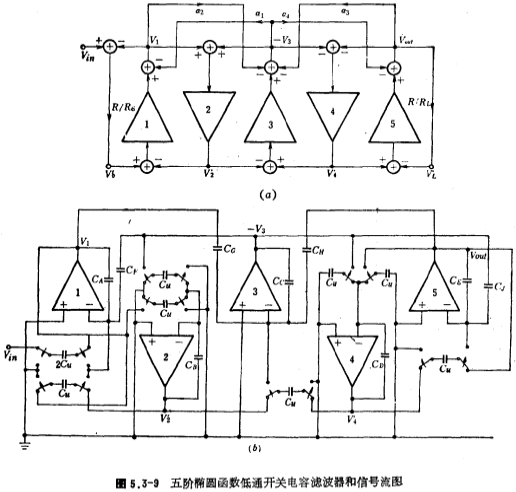
(5.3-19)式中的比例电阻R,通常可根据滤波器的最大动态范围和电容面积最小来进行选取(参看本节四),为简单起见,取R=1欧姆。低通、高通、带通。而图5.3-8中归一化时的电阻Rs和RL通常也是1欧姆,这样,Rs=RL=R=1欧姆,根据图5.3-9a所示的信号流图和Rs=RL=R=1欧姆条件,可以得到图5.3-9b所示的五阶椭圆函数低通开关电容滤波器,对应于图5.3-90.b积分时间常数,并使其相等以及根据(5.3-19)式,可以求得图(b)中各积分器的电容值,其值由下式表示
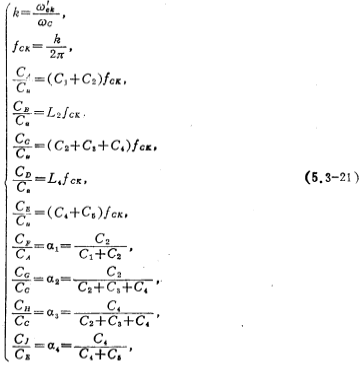
式中ω′ck为实际时钟角须率,ωc为滤波器的截止角频率,fcx为滤波器截止角频率为1弧度/秒时的时钟频率。为使通带增益为0分贝,输入端电容从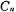 ,扩大到
,扩大到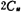 。
。
【例12】设计一个五阶椭圆函数低通开关电容滤波器,主要参数:(1)通带波动RP=0.1分贝;(2)止带最小衰减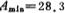 分贝;(3)归一化时止带角频率Ωs=1.20弧度/秒;(4)截止频率fc=3.4千赫;(5)时钟信号频率
分贝;(3)归一化时止带角频率Ωs=1.20弧度/秒;(4)截止频率fc=3.4千赫;(5)时钟信号频率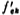 =128千赫。
=128千赫。
解 i.确定图5.3-8电路中各元件值:
查表5.3-3得到
Rs=RL=1欧姆,C1==0.91441,C2=0.31628,L2=1.06516,C2=1.38201,L4=0.60131,C4=1.09329,C5=0.52974。
ii.计算时钟频率f′ck和截止频fc的比值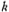 :
:
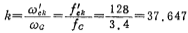
iii.计算归一化时的时钟频率fcx:
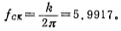
iv.计算电容比:
根据(5.3-21)式
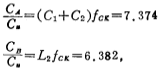
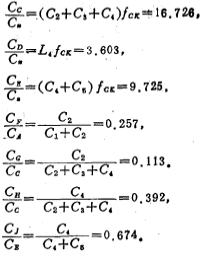
v.计算各电容值:
取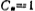 单位电容;CA=7.374单位电容;CB=6.382单位电容;Cc=16.726单位电容;CD=3.603单位电容;CE=9.725单位电容;CF=1.895单位电容;CG=1.890单位电容;CE=6.557单位电容;CJ=6.555单位电容。
单位电容;CA=7.374单位电容;CB=6.382单位电容;Cc=16.726单位电容;CD=3.603单位电容;CE=9.725单位电容;CF=1.895单位电容;CG=1.890单位电容;CE=6.557单位电容;CJ=6.555单位电容。
2、带通滤波器
带通开关电容滤波器的设计步骤:首先,将RLC低通滤波器通过频率变换,求得RLC带通滤波器;其次,列出RLC带通滤波器各节点、支路电压、电流方程式,然后根据电压、电流方程式画出信号流图:最后由信号流图得出带通开关电容滤波器。
RLC二阶归一化低通滤波器如图5.3-10a所示。低通、高通、带通。根据低通到带通的频率变换关系式,将图5.3-10a变换为如图5.3-10b所示的RLC带通滤波器,它的元件值为
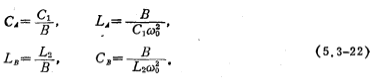
式中C1、L2为RLC二阶归一化低通滤波器元件值,ωo为带通滤波器的中心角频率,B为带通滤波器3分贝带宽。
由图5.3-10b可以得到如下电压、电流方程:
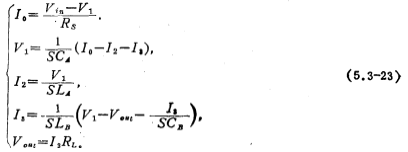
用比例电阻R,将上式中的电流量变为电压量并用t表示,则上式可以改写为
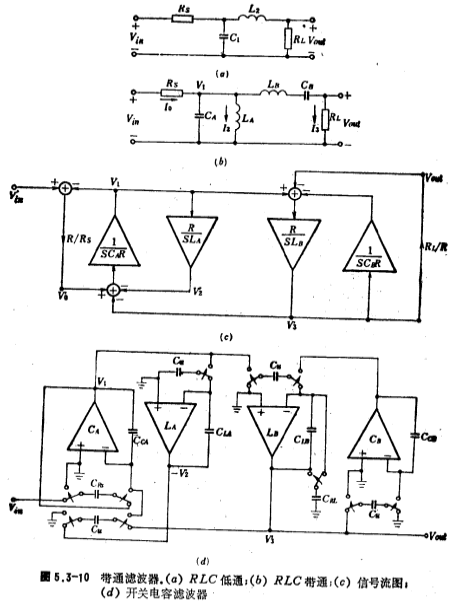
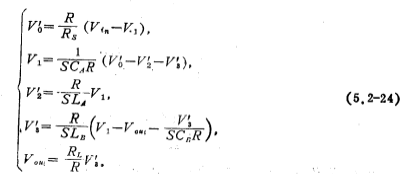
根据(5.3-24)式画出如图5.3-10c所示的信号流图,由此图可以得到带通开关电容滤波器电路,其电路形式如图5.3-10d所示。为简单起见,取Rs=RL=R=1欧姆,这样图中的CRs、CRL与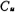 相同,即
相同,即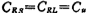 。.该图中各开关电容积分器的电容比值由(5.3-25)式求得,其表示式为
。.该图中各开关电容积分器的电容比值由(5.3-25)式求得,其表示式为
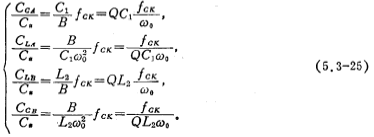
式中Q为带通滤波器的Q值。
【例13】设计一个四阶巴特沃思开关电容滤波器,它的时钟信号频率fcx是带通中心频率fo的20倍,带通的Q值为5。
解 i.计算图5.3-10a的元件值:
由表5.3-1得
Rs=RL=1欧姆,C1=1.4142,L2=1.4142
ii.计算图5.3-10d中各开关电容积分器的电容比值:
由(5.3-25)式,得到如下各积分器的电容比为
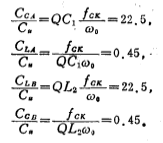
3、高通滤波器
高通开关电容滤波器的设计步骤是:(1)由RLC低通滤波器经频率变换后求得RLC高通滤波器;(2)列出RLC高通滤波器各节点和支路电压、电流方程式:(3)根据电压、电流方程式画出信号流图;(4)由信号流图得出高通开关电容滤波器。图5.3-11a为RLC四阶高通滤波器,它直接由RLC低通滤波器经变换后得到,只要将低通滤波器中的L换成C,C换成L,并且它们之间的元件值互为倒数。
由图5.3-11a得如下电压、电流方程式:

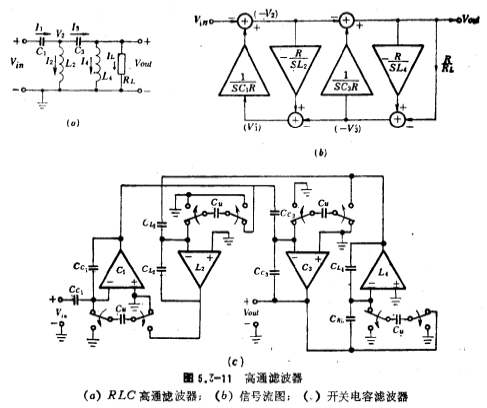
引入比例电阻R,将上式的电流量变为电压量,其关系式为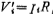 ,这样上式可写成
,这样上式可写成

由(5.3-27)式,画出如图5.3-11b所示的信号流图。根据此信号流图求得四阶高通开关电容滤波器,其电路形式如图5.3-11c所示。低通、高通、带通。为简单起见,取RL=R=1欧姆。该电路的电容比值由下式求得

式中ωc为高通滤波器的截止频率。
【例14】设计一个四阶巴特沃思高通开关电容滤波器,其时钟频率fcx与截止频率fc之比为100。
解 i.计算归一化四阶巴特沃思低通滤波器参数:
由表5.3--2得
RL=1欧姆,L1=1.5307,C2=1,5772,L3=1.0824,C4=0,3827
ii.计算归一化四阶巴特沃思高通滤波器参数:
根据低通滤波器与高通滤波器之间的转换关系,求得高通滤波器中的电感和电容值为
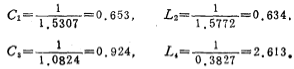
iii.计算5.3-11(c)电路的电容比值:
由(5.3-28)式得
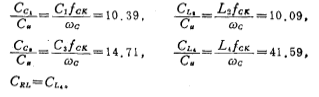
联系方式:邹先生
联系电话:0755-83888366-8022
手机:18123972950
QQ:2880195519
联系地址:深圳市福田区车公庙天安数码城天吉大厦CD座5C1
请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号
请“关注”官方微信公众号:提供 MOS管 技术帮助