电子技术论坛
信息来源: 时间:2020-11-11
MOS加法器(半加器、全加器)的原理及区别
MOS加法器在电子计算机及其它数字系统中,常采用二进制计数,而在二进制数的运算中,加、减、乘、除最终都可以归纳为加法运算。加法运算是计算机中的重要运算。能完成加法运算的电路称为加法器。
一、MOS半加器
如果A、B两数分别表示被加数和加数,用S表示A与B的本位和,用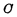 表示向高一位的进位数。A与B相加可归纳如下四种情况:
表示向高一位的进位数。A与B相加可归纳如下四种情况:
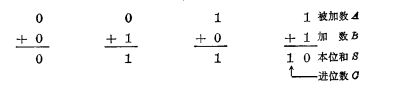
把这四种情况,可归纳为表3-1的真值表。

根据真值表,可以写出逻辑式:

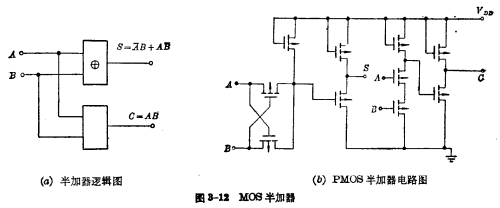
可见本位和S的逻辑关系为“异或”逻辑,进位数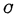 为“与”逻辑。MOS加法器,这种只考虑A、B两敬相加及向高位进位,而不考虑由低位向此位进位的加法电路,称为半加器。图3-12(a)为半加器逻辑图;38-12(b)为半加器电路图。
为“与”逻辑。MOS加法器,这种只考虑A、B两敬相加及向高位进位,而不考虑由低位向此位进位的加法电路,称为半加器。图3-12(a)为半加器逻辑图;38-12(b)为半加器电路图。
二、MOS全加器
若两个多位数相加,除了要考虑对应位的数相加外,还必须考虑与低一位的进位数相加。MOS加法器,因此,两个多位数相加时,每位加法器需要有三个输入端和两个输出端,这种加法器称为全加器。
设两个多位数的第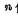 位相对应的数为
位相对应的数为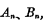 下一位的进位数为
下一位的进位数为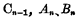 与
与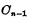 之和为
之和为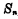 ,高一位的进位数为
,高一位的进位数为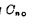 则
则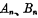
 之和
之和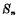 与进位数
与进位数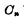 可表示为如下关系式:
可表示为如下关系式:

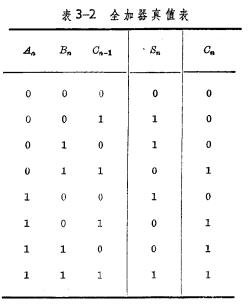
根据以上关系,可列出如表3-2的真值表。根据真值表,当然也可以列出卡诺图进行化简,最后可得出:
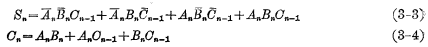
根据(3-3)和(3-4)式画出的逻辑图,输入端要用到反变量,电路结构较为复杂。为了节省门的数目,使电路简化,一般都应充分利用两个逻辑函数间的共同部分。但从(3-3)和(3-4)两式看到,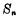 和
和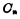 几乎没有共同的部分。MOS加法器如果将
几乎没有共同的部分。MOS加法器如果将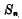 作些变换,就可以找到
作些变换,就可以找到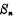 和
和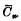 有许多共同的部分。(3-3)式可变换为:
有许多共同的部分。(3-3)式可变换为:
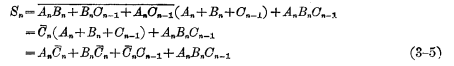
这样用(3-4)和(3-5)式画出来的逻辑图和电路图,输入变量都是原变量,从而避免了输入变量要用反变量的形式,使电路得到简化,如图3-13所示。
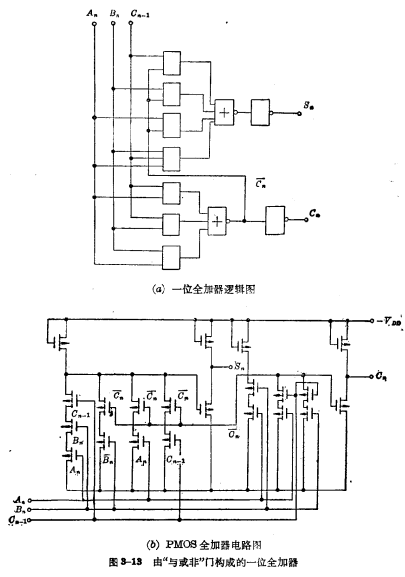
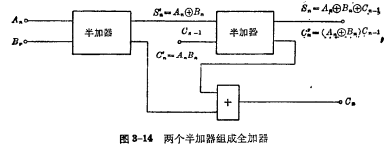
当然,也可以用两个半加器组成一个全加器,其构成方法是这样的:首先将两个多位数的第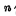 位相对应的
位相对应的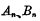 相加,得到本位和
相加,得到本位和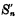 及进位数
及进位数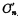 然后,将本位和
然后,将本位和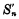 与下一位进过来的
与下一位进过来的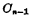 相加,得到和
相加,得到和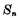 和进位数
和进位数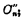 最后,将两个进位数
最后,将两个进位数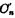 与
与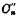 相加,得到向高一位进位的
相加,得到向高一位进位的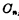 ,如图3-14所示。
,如图3-14所示。
这里必须指出,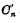 与
与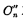 不会同时为1,所以不会产生再进位的问题。
不会同时为1,所以不会产生再进位的问题。
联系方式:邹先生
联系电话:0755-83888366-8022
手机:18123972950
QQ:2880195519
联系地址:深圳市福田区车公庙天安数码城天吉大厦CD座5C1
请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号
请“关注”官方微信公众号:提供 MOS管 技术帮助