MOS管主要参数-mos管低频小信号参数

大家知道，任何器件在频率较高的情况下工作时，器件的电容将起显著的作用。这里所考虑的是指在低频工作时，MOS管的电容效应可以忽略不计，而且输入信号又较小。在这种情况下讨论的参数，称为低频小信号参数。

1、MOS管的跨导g_m 

MOS管的跨导，定义为漏源电压一定时，漏源电流随栅源电压的变化率。MOS管低频小信号。换句话说，就是当栅源输入电压每变化1V所引起漏源电流的变化量。因此，跨导是表征栅电压控制输出电流变化灵敏度的一个物理量，跨导愈大，控制能力愈强，跨导的单位为西门子，符号为S（A/V）。其数学表达式为：

把N沟道MOS管的非饱和区电流公式代入上式，得：

说明非饱和区的跨导是随着VDS增加而增加的。当VDS一定时，g_m与VGS无关。MOS管低频小信号。但实际上k与VGS是有关的。因此，随VGS增加时，g_m将出现减小的趋势。

把NMOS管饱和区的漏电流公式代入（1-54）式，便可得饱和区的跨导为：

把（1-56）式和（1-50）式进行比较，可以看出，饱和区的跨导正好是同一栅压下非饱和区通导电阻的倒数，即：

这是一个很重要的关系式，在下面将经常用到。

从（1-56）式可见，饱和区的跨导g_m与沟道长度L和栅氧化层厚度。成反比，与沟道宽度W成正比。若栅氧化层厚度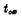一定，则跨导的大小决定于W/L。为了增大跨导，就要使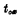小些。因此，在MOS管的制造工艺中，必须注意栅氧化层厚度的控制。

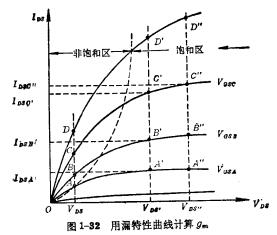
一个MOS管g_m的大小，可以从输出特性曲线上的饱和区求解出来。MOS管低频小信号。从图1-32中看出，饱和区的跨导与VDS无关，而随（VGS一VT）的增加而增加。对于不同的VGS，g_m是不同的。在栅压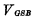附近的跨导，可根据定义计算出来，即：

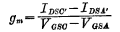
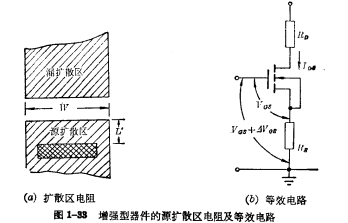
最后还必须指出，跨导还会受到源极串联电阻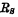的影响，当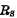较大时，对器件跨导的影响不能忽略，器件原来的跨导将减小。mos管低频小信号,

假设原来器件的跨导为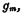若输入信号VGS有一个增量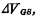则流过管子的电流必有增量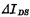。MOS管低频小信号。在图1-38等效电路的输入回路中，可以认为这个增量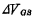分别降落在沟道和源极串联电阻Rs上，即：

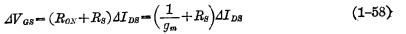
将上式整理：

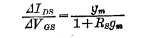
即：

从（1-59）式看到，如果Rs很小，则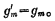当Rs较大时，跨导要下降很多。因此，为了减小源扩散电阻对跨导的影响，应尽量减小Rs。

源扩散电阻可用下式计算：

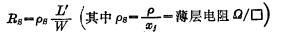
2、漏源输出电导GDS和动态电阻

（1）漏源输出电导 

当循源电压一定时，漏源电流随漏源电压的变化率，就称为MOS管的电导。mos管低频小信号,它是用来表征输出电压对输出电流的控制能力，用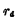表示，其数学表示为：

gDS的单位仍用西门子（S）。

（2）漏源动态电阻

 漏源输出电导的倒数就称为漏源动态电阻，用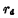表示，这是MOS电路设计中另一个重要参数，其单位为欧姆。数学表示式为：

以前讲到，在饱和区，由于沟道夹断，漏源电流不随漏源电压变化，所以动态电阻应该是无穷大，即：

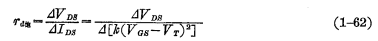
实际上，随着VDS的增大，IDS是略有增加的。MOS管低频小信号。因此，饱和区的动态电阻并不是真的无穷大，而是趋近于一个有限值，一般在10~100kΩ的范围内。

在非饱和区，由子VDS很小，沟道没有夹断，可以认为沟道中各处的厚度相差不多。所以，非饱和区的动态电阻可近似等于直流导通电阻:

3、电压放大系数Kv 

电压放大系数是用来描述栅源输入电压变化所引起的漏源输出电压的变化率，用Kv表示：

经过变换，可得：

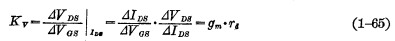
可以看出，电压放大系数与跨导成正比，跨导愈大，放大性能愈好。按理论分析，饱和区的动态电阻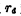趋向无穷大，所以电压放大系数也应趋于无穷大。但实际上饱和区的动态电阻并不是真的无穷大，而是个有限值，所以电压放大系数也是有限的。

在非饱和区（VDS→0），电压放大系数为：

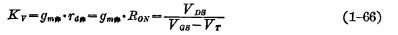
联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助